已知 $M,N$ 是椭圆 $E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)的长轴上的两个定点,椭圆的弦 $AB$ 恒过点 $M$,直线 $AN,BN$ 分别与椭圆 $E$ 交于不同于 $A,B$ 的点 $C,D$,求证:直线 $CD$ 的斜率与直线 $AB$ 的斜率之比为定值.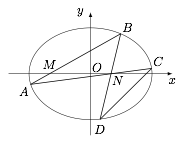

【难度】
【出处】
无
【标注】
【答案】
定值为 $\dfrac{a^2+n^2-2mn}{a^2-n^2}$
【解析】
设 $M(m,0)$,$N(n,0)$,设 $A,B,C,D$ 四点对应的参数分别为 $2\theta_1,2\theta_2,2\theta_3,2\theta_4$,则由椭圆的参数弦方程可得\[\begin{cases}\tan\theta_1\cdot \tan\theta_3=\tan\theta_2\cdot \tan\theta_4=\dfrac{n-a}{n+a},\\
\tan\theta_1\cdot \tan\theta_2=\dfrac{m-a}{m+a},\end{cases}\]从而\[\begin{cases} \tan\theta_2=\dfrac{m-a}{m+a}\cdot \dfrac{1}{\tan\theta_1},\\
\tan\theta_3=\dfrac{n-a}{n+a}\cdot \dfrac{1}{\tan\theta_1},\\
\tan\theta_4=\dfrac{(n-a)(m+a)}{(n+a)(m-a)}\cdot \tan\theta_1,\end{cases}\]因此所求斜率之比为\[\begin{split} \dfrac{\tan(\theta_3+\theta_1)}{\tan(\theta_1+\theta_2)}&=\dfrac{\tan\theta_3+\tan\theta_4}{1-\tan\theta_3\cdot\tan\theta_4}\cdot\dfrac{1-\tan\theta_1\cdot\tan\theta_2}{\tan\theta_1+\tan\theta_2}\\
&=\dfrac{a^2+n^2-2mn}{a^2-n^2}\end{split}\]为定值,原命题得证.
\tan\theta_1\cdot \tan\theta_2=\dfrac{m-a}{m+a},\end{cases}\]从而\[\begin{cases} \tan\theta_2=\dfrac{m-a}{m+a}\cdot \dfrac{1}{\tan\theta_1},\\
\tan\theta_3=\dfrac{n-a}{n+a}\cdot \dfrac{1}{\tan\theta_1},\\
\tan\theta_4=\dfrac{(n-a)(m+a)}{(n+a)(m-a)}\cdot \tan\theta_1,\end{cases}\]因此所求斜率之比为\[\begin{split} \dfrac{\tan(\theta_3+\theta_1)}{\tan(\theta_1+\theta_2)}&=\dfrac{\tan\theta_3+\tan\theta_4}{1-\tan\theta_3\cdot\tan\theta_4}\cdot\dfrac{1-\tan\theta_1\cdot\tan\theta_2}{\tan\theta_1+\tan\theta_2}\\
&=\dfrac{a^2+n^2-2mn}{a^2-n^2}\end{split}\]为定值,原命题得证.
答案
解析
备注