一个多面体的三视图如图所示,其中俯视图中内部的小正方形边长为 $1$,求该多面体的体积.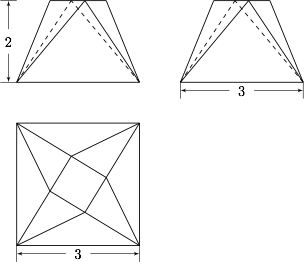

【难度】
【出处】
无
【标注】
【答案】
$\dfrac{20}3+\dfrac {2\sqrt {17}}3$
【解析】
根据题意,该多面体的直观图如图所示为 $EFGH-ABCD$.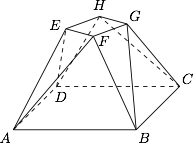 为了方便计算体积,我们计算它的四分之一 $PFG-OBC$,其中 $O,P$ 分别为下底面和上底面的中心,如图.
为了方便计算体积,我们计算它的四分之一 $PFG-OBC$,其中 $O,P$ 分别为下底面和上底面的中心,如图.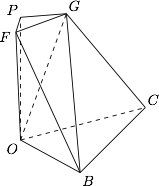 根据题意,有\[\begin{split}V_{ PFG-OBC}&=V_{O-PFG}+V_{FG-OB}+V_{G-OBC}\\ &= \dfrac 13\cdot S_{\triangle PFG}\cdot OP+\dfrac 16\cdot FG\cdot OB\cdot OP\cdot \sin\langle FG,OB\rangle+\dfrac 13\cdot S_{\triangle OBC}\cdot OP.\end{split}\]
根据题意,有\[\begin{split}V_{ PFG-OBC}&=V_{O-PFG}+V_{FG-OB}+V_{G-OBC}\\ &= \dfrac 13\cdot S_{\triangle PFG}\cdot OP+\dfrac 16\cdot FG\cdot OB\cdot OP\cdot \sin\langle FG,OB\rangle+\dfrac 13\cdot S_{\triangle OBC}\cdot OP.\end{split}\]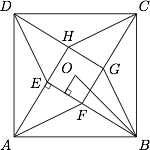 如图,设 $AE=BF=x$,则在直角三角形 $ABE$ 中,有$$x^2+(1+x)^2=9,$$解得$$x=\dfrac{\sqrt{17}-1}2,$$于是$$OB\cdot \sin \langle FG,OB\rangle= \dfrac{\sqrt{17}}2,$$因此$$V_{ PFG-OBC}=\dfrac 53+\dfrac{\sqrt{17}}6,$$进而可得$$V_{EFGH-ABCD}=4V_{PFG-OBC}=\dfrac{20}3+\dfrac {2\sqrt {17}}3.$$
如图,设 $AE=BF=x$,则在直角三角形 $ABE$ 中,有$$x^2+(1+x)^2=9,$$解得$$x=\dfrac{\sqrt{17}-1}2,$$于是$$OB\cdot \sin \langle FG,OB\rangle= \dfrac{\sqrt{17}}2,$$因此$$V_{ PFG-OBC}=\dfrac 53+\dfrac{\sqrt{17}}6,$$进而可得$$V_{EFGH-ABCD}=4V_{PFG-OBC}=\dfrac{20}3+\dfrac {2\sqrt {17}}3.$$
 为了方便计算体积,我们计算它的四分之一 $PFG-OBC$,其中 $O,P$ 分别为下底面和上底面的中心,如图.
为了方便计算体积,我们计算它的四分之一 $PFG-OBC$,其中 $O,P$ 分别为下底面和上底面的中心,如图. 根据题意,有\[\begin{split}V_{ PFG-OBC}&=V_{O-PFG}+V_{FG-OB}+V_{G-OBC}\\ &= \dfrac 13\cdot S_{\triangle PFG}\cdot OP+\dfrac 16\cdot FG\cdot OB\cdot OP\cdot \sin\langle FG,OB\rangle+\dfrac 13\cdot S_{\triangle OBC}\cdot OP.\end{split}\]
根据题意,有\[\begin{split}V_{ PFG-OBC}&=V_{O-PFG}+V_{FG-OB}+V_{G-OBC}\\ &= \dfrac 13\cdot S_{\triangle PFG}\cdot OP+\dfrac 16\cdot FG\cdot OB\cdot OP\cdot \sin\langle FG,OB\rangle+\dfrac 13\cdot S_{\triangle OBC}\cdot OP.\end{split}\] 如图,设 $AE=BF=x$,则在直角三角形 $ABE$ 中,有$$x^2+(1+x)^2=9,$$解得$$x=\dfrac{\sqrt{17}-1}2,$$于是$$OB\cdot \sin \langle FG,OB\rangle= \dfrac{\sqrt{17}}2,$$因此$$V_{ PFG-OBC}=\dfrac 53+\dfrac{\sqrt{17}}6,$$进而可得$$V_{EFGH-ABCD}=4V_{PFG-OBC}=\dfrac{20}3+\dfrac {2\sqrt {17}}3.$$
如图,设 $AE=BF=x$,则在直角三角形 $ABE$ 中,有$$x^2+(1+x)^2=9,$$解得$$x=\dfrac{\sqrt{17}-1}2,$$于是$$OB\cdot \sin \langle FG,OB\rangle= \dfrac{\sqrt{17}}2,$$因此$$V_{ PFG-OBC}=\dfrac 53+\dfrac{\sqrt{17}}6,$$进而可得$$V_{EFGH-ABCD}=4V_{PFG-OBC}=\dfrac{20}3+\dfrac {2\sqrt {17}}3.$$
答案
解析
备注