已知不等式 $a\leqslant \dfrac 34x^2-3x+4\leqslant b$ 的解集恰好是 $[a,b]$，求 $a,b$ 的值．
【难度】
【出处】
无
【标注】
【答案】
$ a=0,b=4 $
【解析】
题中不等式的解是函数 $f(x)=\dfrac 34x^2-3x+4$ 的图象在直线 $y=a$ 与直线 $y=b$ 之间的部分在 $x$ 轴上的投影所表示的区间．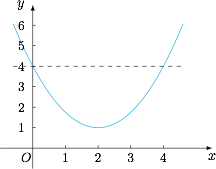
容易确定 $a\leqslant 1$，否则投影区间不连续，与题意不符．
于是 $a,b$ 是方程 $f(x)=b$ 的两根，根据韦达定理，有$$\begin{cases}a+b=4,\\ab=\dfrac 43(4-b),\end{cases}$$解得$$a=0\land b=4.$$
容易确定 $a\leqslant 1$，否则投影区间不连续，与题意不符．于是 $a,b$ 是方程 $f(x)=b$ 的两根，根据韦达定理，有$$\begin{cases}a+b=4,\\ab=\dfrac 43(4-b),\end{cases}$$解得$$a=0\land b=4.$$
答案
解析
备注
