如图,在 $\triangle ABC$ 中,$AB=AC$,$I$ 为 $\triangle ABC$ 的内心.以 $A$ 为圆心,$AB$ 为半径作圆 $\Gamma_1$,以 $I$ 为圆心,$IB$ 为半径作圆 $\Gamma_2$,过点 $B$、$I$ 的圆 $\Gamma_3$ 与 $\Gamma_1$、$\Gamma_2$ 分别交于点 $P$、$Q$(不同于点 $B$).设 $IP$ 与 $BQ$ 交于点 $R$.证明:$BR \perp CR$.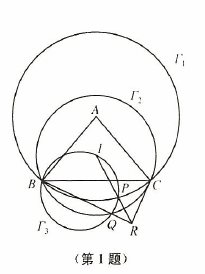

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注