解方程 $x^3-3x=\sqrt{x+2}$．
【难度】
【出处】
无
【标注】
【答案】
$\left\{2,2\cos\dfrac{4\pi}7,2\cos\dfrac{4\pi}5\right\}$
【解析】
分别画出 $y=x^3-3x$ 与 $y=\sqrt{x+2}$ 的图象：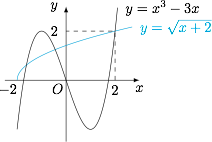
注意到$$4\cdot\left(\dfrac x2\right)^3-3\cdot\dfrac{x}{2}=\sqrt{\dfrac{\dfrac x2+1}{2}},$$联想余弦的三倍角和半角公式，令 $\dfrac x2=\cos \theta$，$\theta\in [0,\pi]$，则$$4\cos^3\theta-3\cos\theta=\sqrt{\dfrac{1+\cos\theta}{2}},$$即$$\cos{3\theta}=\cos\dfrac{\theta}{2},$$解得$$3\theta=\dfrac{\theta}{2} \lor 3\theta=2\pi-\dfrac{\theta}{2} \lor 3\theta=2\pi+\dfrac{\theta}{2},$$即$$\theta=0,\dfrac{4\pi}{7},\dfrac{4\pi}5,$$于是$$x=2,2\cos\dfrac{4\pi}7,2\cos\dfrac{4\pi}5.$$
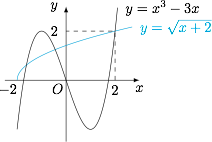注意到$$4\cdot\left(\dfrac x2\right)^3-3\cdot\dfrac{x}{2}=\sqrt{\dfrac{\dfrac x2+1}{2}},$$联想余弦的三倍角和半角公式，令 $\dfrac x2=\cos \theta$，$\theta\in [0,\pi]$，则$$4\cos^3\theta-3\cos\theta=\sqrt{\dfrac{1+\cos\theta}{2}},$$即$$\cos{3\theta}=\cos\dfrac{\theta}{2},$$解得$$3\theta=\dfrac{\theta}{2} \lor 3\theta=2\pi-\dfrac{\theta}{2} \lor 3\theta=2\pi+\dfrac{\theta}{2},$$即$$\theta=0,\dfrac{4\pi}{7},\dfrac{4\pi}5,$$于是$$x=2,2\cos\dfrac{4\pi}7,2\cos\dfrac{4\pi}5.$$
答案
解析
备注
