题目 已知椭圆 $E:\dfrac{x^2}2+y^2=1$．设 $A_2$ 为椭圆的右顶点． 问题1 过 $A_2$ 且互相垂直的两条直线分别交椭圆 $E$ 于另两点 $A,B$，直线 $AB$ 是否过定点？请说明理由．<img src="/static/images/c54a16b8348c35facc71650ffc420375.png" class="img-responsive" /> 答案1 直线 $AB$ 恒过定点 $\left(\dfrac{\sqrt 2}3,0\right)$ 解析1 设直线 $A_2A$ 的方程为 $x=my+\sqrt 2$，$A(x_1,y_1)$，$B(x_2,y_2)$，直线 $AB$ 交 $x$ 轴于点 $T(t,0)$．<br/>联立直线 $A_2A$ 与椭圆 $E$ 的方程，可得$$(m^2+2)y^2+2\sqrt 2my=0,$$于是$$y_1=\dfrac{-2\sqrt 2m}{m^2+2},$$类似地，可得$$y_2=\dfrac{2\sqrt 2m}{2m^2+1}.$$于是由$$\dfrac{y_1-0}{x_1-t}=\dfrac{y_2-0}{x_2-t}$$可得\[\begin{split} t=&\dfrac{x_1y_2-x_2y_1}{y_2-y_1}\\=&\dfrac{(my_1+\sqrt 2)y_2-\left(-\dfrac 1my_2+\sqrt 2\right)y_1}{y_2-y_1}\\=&\dfrac{\left(m+\dfrac 1m\right)\cdot y_1y_2}{y_2-y_1}+\sqrt 2 =\dfrac{\sqrt 2}3\end{split} \]为定值，因此直线 $AB$ 恒过定点 $\left(\dfrac{\sqrt 2}3,0\right)$． 备注1 问题2 设直线 $l:x=2$，$F$ 为椭圆的右焦点，过 $F$ 的直线交椭圆 $E$ 于 $P,Q$．设 $G$ 为直线 $l$ 上的任意一点，直线 $PG,FG,QG$ 的斜率分别为 $k_1,k_2,k_3$，求证：$k_1,k_2,k_3$ 成等差数列．<img src="/static/images/466ca7e8072c0c881d010bf6709c32a5.png" class="img-responsive" /> 答案2 略 解析2 设直线 $PQ:x=my+1$，$P(x_1,y_1)$，$Q(x_2,y_2)$，则联立直线 $PQ$ 与椭圆 $E$ 的方程，有$$(m^2+2)y^2+2my-1=0,$$于是$$y_1+y_2=-\dfrac{2m}{m^2+2},y_1y_2=-\dfrac{1}{m^2+2}.$$设 $G(2,t)$，则欲证明结论等价于$$\dfrac{t-y_1}{2-x_1}+\dfrac{t-y_2}{2-x_2}=2t,$$即$$(t-y_1)(1-my_2)+(t-y_2)(1-my_1)=2t(1-my_1)(1-my_2),$$也即$$(tm-1)\left[(y_1+y_2)-2m\cdot y_1y_2\right]=0.$$事实上，由$$y_1+y_2=-\dfrac{2m}{m^2+2},y_1y_2=-\dfrac{1}{m^2+2},$$可得$$(y_1+y_2)-2m\cdot y_1y_2=0,$$因此原命题得证． 备注2 问题3 设直线 $l:x=2$，$F$ 为椭圆的右焦点，过 $F$ 的直线交椭圆 $E$ 于 $P,Q$．设 $A_1$ 是椭圆的左顶点，直线 $A_1P,A_1Q$ 分别与直线 $l$ 交于点 $M,N$，求证：直线 $FM$ 和直线 $FN$ 的斜率之积为定值．<img src="/static/images/56fd6ef81bc47d924c35c18e89774ba8.png" class="img-responsive" /> 答案3 略 解析3 设直线 $PQ:x=my+1$，$P(x_1,y_1)$，$Q(x_2,y_2)$，则联立直线 $PQ$ 与椭圆 $E$ 的方程，有$$(m^2+2)y^2+2my-1=0,$$于是$$y_1+y_2=-\dfrac{2m}{m^2+2},y_1y_2=-\dfrac{1}{m^2+2}.$$设点 $M$、$N$ 的纵坐标为 $y_M$、$y_N$，<br/>则由$$\dfrac{y_M}{2+\sqrt 2}=\dfrac{y_1}{x_1+\sqrt 2},$$可得$$y_M=\dfrac{\left(2+\sqrt 2\right)y_1}{x_1+\sqrt 2}=\dfrac{\left(2+\sqrt 2\right)y_1}{my_1+1+\sqrt 2},$$类似地，有$$y_N=\dfrac{\left(2+\sqrt 2\right)y_2}{my_2+1+\sqrt 2}.$$因此可得直线 $FM$ 与直线 $FN$ 的斜率之积\[\begin{split} k_{FM}\cdot k_{FN}&=\dfrac{y_M-0}{2-1}\cdot\dfrac{y_N-0}{2-1}\\&=\dfrac{\left(2+\sqrt 2\right)^2y_1y_2}{(my_1+1+\sqrt 2)(my_2+1+\sqrt 2)}\\&=\dfrac{\left(2+\sqrt 2\right)^2\cdot y_1y_2}{m^2y_1y_2+(1+\sqrt 2)m\cdot (y_1+y_2)+(1+\sqrt 2)^2}\\& =-1\end{split}\]为定值，原命题得证． 备注3 问题4 设直线 $l:x=2$，$F$ 为椭圆的右焦点，过 $F$ 的直线交椭圆 $E$ 于 $P,Q$．设 $H(2,\sqrt 7)$ 为直线 $l$ 上一点，若向量 $\overrightarrow{HP}$ 与向量 $\overrightarrow{HQ}$ 的夹角为 $45^\circ$，求直线 $PQ$ 的斜率．<img src="/static/images/2204e3dd2ce5fc7df47dced68e62b3be.png" class="img-responsive" /> 答案4 $-\dfrac{\sqrt 7}7$ 解析4 设直线 $PQ:x=my+1$，$P(x_1,y_1)$，$Q(x_2,y_2)$，则联立直线 $PQ$ 与椭圆 $E$ 的方程，有$$(m^2+2)y^2+2my-1=0,$$于是$$y_1+y_2=-\dfrac{2m}{m^2+2},y_1y_2=-\dfrac{1}{m^2+2}.$$本题的背景为一般结论：从准线上一点看椭圆的张角 $\theta$ 满足$$\tan \theta=\dfrac{2e}{(1-e^2)\sqrt{1+m^2}},$$依此结论不难得到 $m$ 的值应该为 $-\sqrt 7$．<br/><sol>利用到角公式直接计算</sol><br/>根据题意，有$$\left|\dfrac{\dfrac{y_1-\sqrt 7}{my_1-1}-\dfrac{y_2-\sqrt 7}{my_2-1}}{1+\dfrac{y_1-\sqrt 7}{my_1-1}\cdot \dfrac{y_2-\sqrt 7}{my_2-1}}\right|=1,$$即$$\left[(my_1-1)(my_2-1)+(y_1-\sqrt 7)(y_2-\sqrt 7)\right]^2=\left[(my_1-1)(y_2-\sqrt 7)-(my_2-1)(y_1-\sqrt 7)\right]^2,$$整理得$$(9m^2+2\sqrt 7m+15)^2=8(m^2+1)(7m^2-2\sqrt 7m+1),$$令 $t=m+\sqrt 7$，则可整理得$$t^2\left(25t^2-48\sqrt 7t+192\right)=0,$$因此 $m$ 的值为 $-\sqrt 7$，直线 $PQ$ 的斜率为 $-\dfrac{\sqrt 7}7$．<br/><sol>利用到角公式结合第2小题结论计算</sol><br/>设直线 $HP,HQ$ 的斜率分别为 $k_1,k_2$，则根据题意有$$\left|\dfrac{k_1-k_2}{1+k_1k_2}\right|=1,$$即$$(k_1+k_2)^2-4k_1k_2=(k_1k_2+1)^2,$$根据第2小题结论有$$k_1+k_2=2\sqrt 7,$$由以上两方程可得$$(k_1k_2)^2+6\cdot k_1k_2-27=0,$$从而$$k_1k_2=3\lor k_1k_2=-9,$$显然 $k_1,k_2>0$，因此 $k_1k_2=3$．<br/>设过点 $H$ 的直线方程为$$y-\sqrt 7=k(x-2),$$则根据等效判别式，可得该直线与椭圆 $E$ 相切即$$2k^2+1-(-2k+\sqrt 7)^2=0,$$即$$k^2-2\sqrt 7k+3=0.$$因此 $k_1,k_2$ 是该方程的两个根，也即直线 $HP,HQ$ 均为椭圆的切线，而直线 $PQ$ 为点 $H$ 对应的极线$$x+\sqrt 7y=1,$$因此直线 $PQ$ 的斜率为 $-\dfrac{\sqrt 7}7$． 备注4 问题5 设 $A_{3}$ 为椭圆的上顶点，圆 $I:\left(x-\dfrac 23\right)^2+y^2=r^2$ 是椭圆 $E$ 的内接三角形 $A_1B_1C_1$ 的内切圆，过 $A_3$ 作圆 $I$ 的两条切线分别交椭圆于 $B_3,C_3$．求 $r$ 的值并证明直线 $B_3C_3$ 与圆 $I$ 相切．<img src="/static/images/0f9d1bab99c343d3698c8574315ba54a.png" class="img-responsive" /> 答案5 $r=\dfrac{\sqrt 2}3$ 解析5 设直线 $A_1C_1,B_1C_1$ 上的切点分别为 $J,K$，连接 $IJ$，如图．由对称性知 $B_1C_1$ 与 $x$ 轴垂直．<img src="/static/images/fab59090260cbcdd47a2e631701a2ca5.png" class="img-responsive" />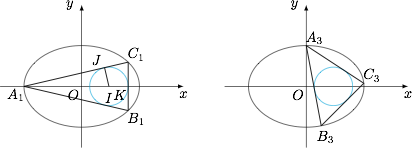设 $C_1(n+r,y)$，其中 $n=\dfrac 23$，则由$$\dfrac{IJ}{A_1J}=\dfrac{C_1K}{A_1K}$$得$$\dfrac{r}{\sqrt{\left(\sqrt 2+n\right)^2-r^2}}=\dfrac{y}{\sqrt 2+n+r},$$所以$$y=\dfrac{r\cdot \sqrt{(\sqrt 2+n)+r}}{\sqrt{(\sqrt 2+n)-r}},$$又由$$\dfrac{(n+r)^2}{2}+y^2=1,$$得$$y=\dfrac{\sqrt{\sqrt 2-(n+r)}\cdot\sqrt{\sqrt 2+(n+r)}}{\sqrt 2},$$由以上两式得$$\dfrac{r}{\sqrt{(\sqrt 2+n)-r}}=\dfrac{\sqrt{(\sqrt 2-n)-r}}{\sqrt 2},$$整理得$$r^2+2\sqrt 2 r-2+n^2=0,$$于是解得 $r=\dfrac{\sqrt 2}3$．<br/>设圆 $I$ 的过点 $A_3$ 的切线为 $y=kx+1$，即$$kx-y+1=0,$$则 $A_3B_3,A_3C_3$ 的斜率 $k_1,k_2$ 是方程$$\dfrac{\left|\dfrac 23k+1\right|}{\sqrt {1+k^2}}=\dfrac{\sqrt 2}3,$$即$$2k^2+12k+7=0$$的根，于是$$k_1+k_2=-6,k_1k_2=\dfrac 72.$$两切线方程为$$(y-k_1x-1)(y-k_2x-1)=0,$$即$$(y-1)^2-x(y-1)(k_1+k_2)+k_1k_2x^2=0,$$也即$$-\dfrac 72x^2=(y-1)(y-1+6x).$$将椭圆方程变形为$$-\dfrac{x^2}{2}=(y-1)(y+1),$$将以上两式联立（即相除）得直线 $B_3C_3$ 的方程$$7=\dfrac{y-1+6x}{y+1},$$即$$3x-3y-4=0,$$因此圆心 $I\left(\dfrac 23,0\right)$ 到直线 $B_3C_3$ 的距离$$d=\dfrac{\left|3\times\dfrac 23-4\right|}{\sqrt{3^2+(-3)^2}}=\dfrac{\sqrt 2}3,$$与半径 $r$ 相等，因此直线 $B_3C_3$ 与圆 $I$ 相切，命题得证． 备注5 <case>注一</case>这个连环解析几何试题是我偶然从一个QQ讨论群中得到的题目，是训练解析几何解题能力的绝佳练习材料．解决这些问题无需花哨的技巧，只需要潜心运算，可以在提高解题能力的同时修身养性，达到一举两得的效果．<br/><case>注二</case>最后一小题的背景为彭赛列闭合定理．<br/>每日一题[400]五仁月饼．