如图,$A,B$ 为椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 和双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 的公共顶点,$P,Q$ 分别为双曲线和椭圆上不同于 $A,B$ 的动点,且满足 $\overrightarrow{AP}+\overrightarrow{BP}=\lambda\left(\overrightarrow{AQ}+\overrightarrow{BQ}\right)$($\lambda\in\mathbb R$,$|\lambda|>1$),求证: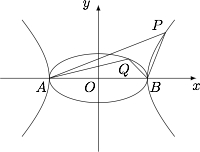

【难度】
【出处】
2015年全国高中数学联赛湖南省预赛
【标注】
-
三点 $O,P,Q$ 在同一直线上;标注答案略解析因为 $O$ 为原点,所以$$\overrightarrow{AP}+\overrightarrow{BP}=2\overrightarrow{OP} , \overrightarrow{AQ}+\overrightarrow{BQ}=2\overrightarrow{OQ},$$又$$\overrightarrow{AP}+\overrightarrow{BP}=\lambda\left(\overrightarrow{AQ}+\overrightarrow{BQ}\right),$$故 $\overrightarrow{OP}=\lambda\overrightarrow{OQ}$,于是 $O,P,Q$ 三点共线.
-
若直线 $AP,BP,AQ,BQ$ 的斜率分别是 $k_1,k_2,k_3,k_4$,则 $k_1+k_2+k_3+k_4$ 是定值.标注答案为定值 $0$解析设 $P(x_1,y_1),Q(x_2,y_2)$,则$$x_1^2-a^2=\dfrac{a^2}{b^2}y_1^2 , x_2^2-a^2=-\dfrac{a^2}{b^2}y_2^2.$$所以$$k_1+k_2=\dfrac{y_1}{x_1+a}+\dfrac{y_1}{x_1-a}=\dfrac{2x_1y_1}{x_1^2-a^2}=\dfrac{2b^2}{a^2}\cdot\dfrac{x_1}{y_1}.$$同理可得$$k_3+k_4=-\dfrac{2b^2}{a^2}\cdot\dfrac{x_2}{y_2}.$$由 $(1)$ 可知,$O,P,Q$ 三点共线,所以$$\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2},$$故$$k_1+k_2+k_3+k_4=\dfrac{2b^2}{a^2}\left(\dfrac{x_1}{y_1}-\dfrac{x_2}{y_2}\right)=0,$$即 $k_1+k_2+k_3+k_4$ 为定值 $0$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2