$\triangle ABC$ 内接于 $\odot O$,$P$ 在 $\overparen {BC}$ 上,$K$ 在 $AP$ 上,$BK$ 平分 $\angle ABC$,$\Omega$ 为 $\triangle KPC$ 外接圆,$\Omega$ 与 $AC$ 交于异于 $C$ 的点 $D$,与 $BD$ 交于异于 $D$ 的点 $E$,直线 $PE$ 与 $AB$ 交于 $F$.求证:$\angle ABC=2\angle FCB$.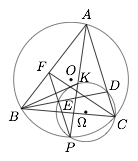

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注