$\triangle ABC$ 的内切圆 $\varGamma$ 与 $BC$ 边切于 $D$,$DD'$ 为 $\varGamma $ 的直径.$AD$ 上的点 $X$ 满足 $XD' \perp DD'$,作 $X$ 关于 $\varGamma$ 的另一条切线与 $\varGamma$ 切于异于 $D'$ 的点 $N$,如图.求证:$\triangle BCN$ 的外接圆与 $\varGamma$ 内切于点 $N$.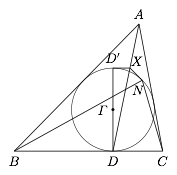

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注