$\triangle ABC$ 中,$BC$ 的延长线上有一点 $D$,满足 $AC=CD$,作 $\triangle ACD$ 的外接圆 $\varGamma_1$ 及以 $BC$ 为直径的圆 $\varGamma_2$,$\varGamma_1$ 与 $\varGamma_2$ 有异于 $C$ 的交点 $P$.直线 $BP$ 交边 $AC$ 于点 $E$,直线 $CP$ 交边 $AB$ 于点 $F$,求证:$D$,$E$,$F$ 三点共线.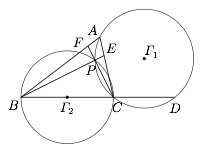

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注