$\triangle ABC$ 内切圆 $\odot I$,切点为 $D,E,F$,如图.直线 $DE$ 与 $AB$ 交于 $P$,直线 $DF$ 与 $AC$ 交于 $Q$,直线 $BE$ 与 $CF$ 交于 $J$,求证:$IJ \perp PQ$.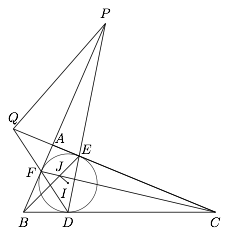

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注