在四边形 $ABCD$ 中，$AB=AD$，$\angle CAB=3\angle CAD$，$\angle ACD=\angle CBD$ 且为锐角，求 $\tan\angle ACD$．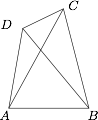
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\sqrt 3}3$
【解析】
设 $AC$ 与 $BD$ 交于 $E$，取 $BD$ 的中点 $F$，设 $\angle CAD=\alpha$，$\angle ACD=\beta$，$AD=AB=1$，如图．
在三角形 $ABD$ 中，有$$BD=2\sin{2\alpha},$$在三角形 $ACD$ 中，由正弦定理有$$CD=\dfrac{\sin\alpha}{\sin\beta},$$在三角形 $BCD$ 中，有$$\angle DCB=\angle ECB+\beta=\angle DEC=\dfrac{\pi}2-\alpha,$$从而应用正弦定理$$\dfrac{CD}{\sin\beta}=\dfrac{BD}{\sin\left(\dfrac{\pi}{2}-\alpha\right)},$$将转化后的条件代入，即得$$\sin\beta=\dfrac 12,$$于是所求值为 $\dfrac{\sqrt 3}3$．
在三角形 $ABD$ 中，有$$BD=2\sin{2\alpha},$$在三角形 $ACD$ 中，由正弦定理有$$CD=\dfrac{\sin\alpha}{\sin\beta},$$在三角形 $BCD$ 中，有$$\angle DCB=\angle ECB+\beta=\angle DEC=\dfrac{\pi}2-\alpha,$$从而应用正弦定理$$\dfrac{CD}{\sin\beta}=\dfrac{BD}{\sin\left(\dfrac{\pi}{2}-\alpha\right)},$$将转化后的条件代入，即得$$\sin\beta=\dfrac 12,$$于是所求值为 $\dfrac{\sqrt 3}3$．
答案
解析
备注
