圆 $\omega_1 ,\omega_2,\omega_3$ 两两相离.设 $\omega_1$ 与 $\omega_2$ 的外公切线交点为 $A$,$\omega_2$ 与 $\omega_3$ 的外公切线交点为 $B$,$\omega_3$ 与 $\omega_1$ 的外公切线交点为 $C$.求证:$A,B,C$ 共线.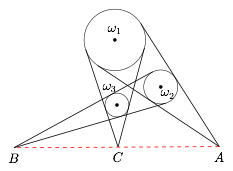

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $\omega_1,\omega_2,\omega_3$ 的圆心分别为 $O_1,O_2,O_3$,考虑 $\triangle O_1O_2O_3$,$ABC$ 是它的截线,因此可以利用梅涅劳斯定理的逆定理证明共线.只需证明\[\dfrac{O_1A}{AO_2}\cdot \dfrac{O_2B}{BO_2}\cdot \dfrac{O_2C}{CO_3}=1,\]而\[\dfrac{O_1A}{AO_2},\dfrac{O_2B}{BO_2}, \dfrac{O_2C}{CO_3}\]可以转化为对应的圆的半径之比,因此命题得证.
答案
解析
备注