不等边三角形 $ABC$ 中,$\angle A$ 内的旁切圆与边 $AB,AC$ 分别切于 $A_1,A_2$,$\angle B$ 内的旁切圆与边 $BC,BA$ 分别切于 $B_1,B_2$,$\angle C$ 内的旁切圆与边 $CA,CB$ 分别切于 $C_1,C_2$.设直线 $A_1A_2$ 与直线 $BC$ 交于 $A_3$,直线 $B_1B_2$ 与直线 $AC$ 交于 $B_3$,直线 $C_1C_2$ 与直线 $AB$ 交于 $C_3$.求证:$A_3,B_3,C_3$ 共线.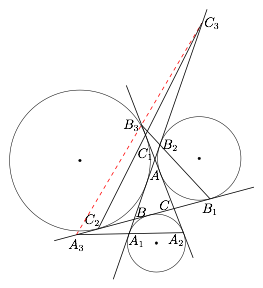

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
要证明共线,可将 $A_3B_3C_3$ 视为截线对 $\triangle ABC$ 用梅涅劳斯逆定理,而直线 $BC$ 上的比例关系可以用截线 $AA_1A_2$ 的梅涅劳斯定理得到,事实上\[\dfrac{AA_1}{A_1B}\cdot\dfrac{BA_3}{A_3C}\cdot\dfrac{CA_2}{A_2A}=1\]而由 $A_1,A_2$ 分别为旁切圆切点知 $AA_1=AA_2$,故\[\dfrac{BA_3}{A_3C}=\dfrac{BA_1}{A_2C}\]再利用旁切圆的性质,$BA_1=\dfrac{AC+CB-AB}{2}=AB_2$,同理 $CA_2=AC_1$,$BC_2=CB_1$,将三个对称的式子相乘即可
答案
解析
备注