$\triangle ABC$ 被直线 $l$ 所截,交于 $BC$ 延长线上点 $D$ 及 $AC$ 边上点 $E$,$AB$ 边上点 $F$.在 $\triangle ABC$ 外接圆 $\Omega$ 上,作三条弦 $A_1A,B_1B,C_1C$ 均与 $l$ 平行.求证:$A_1D,B_1E,C_1F$ 共点.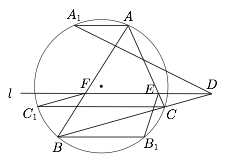

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
考虑过 $\Omega$ 圆心且垂直于 $l$ 的直线 $l'$,由圆的对称性知 $A,A_1,B,B_1,C,C_1$ 是三对关于直线 $l'$ 的对称点,作出 $D,E,F$ 分别关于 $l'$ 的对称点 $D_1,E_1,F_1$,只需证明 $AD_1,BE_1,CF_1$ 三线共点,我们来用角元塞瓦定理
由正弦定理,$\dfrac{sin\angle BAD_1}{sin\angle D_1AC}=\dfrac{D_1F}{D_1E}\cdot\dfrac{AE}{AF}$
将与上式对称的三个式子相乘,注意由于对称性,$D_1F=DF_1,D_1E=DE_1,E_1F=EF_1$,而由梅涅劳斯定理又有\[\dfrac{AE}{EC}\cdot\dfrac{CD}{DB}\cdot\dfrac{BF}{FA}=1\]就可以由角元塞瓦定理逆定理证明结论
由正弦定理,$\dfrac{sin\angle BAD_1}{sin\angle D_1AC}=\dfrac{D_1F}{D_1E}\cdot\dfrac{AE}{AF}$
将与上式对称的三个式子相乘,注意由于对称性,$D_1F=DF_1,D_1E=DE_1,E_1F=EF_1$,而由梅涅劳斯定理又有\[\dfrac{AE}{EC}\cdot\dfrac{CD}{DB}\cdot\dfrac{BF}{FA}=1\]就可以由角元塞瓦定理逆定理证明结论
答案
解析
备注