四边形 $ABCF$ 中,$BF=AF+FC$.$D$ 在边 $BC$ 上,$E$ 在 $BA$ 延长线上.$BD=BE=AC$.若 $AF \cdot CD=FC \cdot AE$,求证:四边形 $ABCF$ 有外接圆.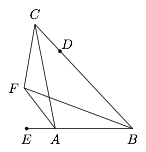

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
与边长乘积相关的四点共圆证明方法我们首先想到托勒密定理逆定理,只需证明 $AB\cdot CF+AF\cdot BC=AC\cdot BF$
由题设 $BD=BE=AC,BF=AF+FC$,上式变成 $AB\cdot CF+AF\cdot BC=BD\cdot AF+BE\cdot FC$,整理即只需证明 $AF\cdot CD=FC\cdot AE$,这恰好是题设
由题设 $BD=BE=AC,BF=AF+FC$,上式变成 $AB\cdot CF+AF\cdot BC=BD\cdot AF+BE\cdot FC$,整理即只需证明 $AF\cdot CD=FC\cdot AE$,这恰好是题设
答案
解析
备注