已知 $\triangle ABC$ 中,$B(-1,0)$,$C(1,0)$.设点 $G,I$ 分别为 $\triangle ABC$ 的重心和内心,且 $GI\parallel BC$,求 $A$ 点的轨迹方程.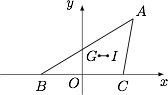

【难度】
【出处】
无
【标注】
【答案】
$\dfrac{x^2}4+\dfrac{y^2}{3}=1,y\neq 0$
【解析】
由于 $GI\parallel BC$,于是$$S_{\triangle IBC}=S_{\triangle GBC}=\dfrac 13S_{\triangle ABC},$$进而\[\dfrac{S_{\triangle ABC}}{S_{\triangle IBC}}=\dfrac{AB+BC+CA}{BC}=3,\]于是\[AB+AC=2BC=4.\]根据椭圆的定义可知,$A$ 点的轨迹方程为$$\dfrac{x^2}4+\dfrac{y^2}{3}=1,y\neq 0.$$
答案
解析
备注