已知 $\triangle ABC$ 中，$B(-1,0)$，$C(1,0)$．设点 $G,I$ 分别为 $\triangle ABC$ 的重心和内心，且 $GI\parallel BC$，求 $A$ 点的轨迹方程．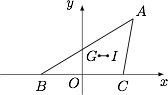
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{x^2}4+\dfrac{y^2}{3}=1,y\neq 0$
【解析】
如图，延长 $AI$ 交 $BC$ 于点 $D$．
根据重心和内心的性质，有$$\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AI}{DI}=\dfrac {AG}{GO}=\dfrac 21,$$于是$$\dfrac{AB+AC}{BD+DC}=2,$$即\[AB+AC=4,\]因此所求 $A$ 点的轨迹方程为\[\dfrac{x^2}4+\dfrac{y^2}{3}=1,y\neq 0.\]
根据重心和内心的性质，有$$\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AI}{DI}=\dfrac {AG}{GO}=\dfrac 21,$$于是$$\dfrac{AB+AC}{BD+DC}=2,$$即\[AB+AC=4,\]因此所求 $A$ 点的轨迹方程为\[\dfrac{x^2}4+\dfrac{y^2}{3}=1,y\neq 0.\]
答案
解析
备注
