在正方体 $ABCD-A_1B_1C_1D_1$ 中，棱 $AB$ 的中点为 $P$．若光线从 $P$ 出发，依次经过三个侧面 $BCC_1B_1$，$DCC_1D_1$，$ADD_1A_1$ 反射后，落到侧面 $ABB_1A_1$（不包括边界）上，求入射光线 $PQ$ 与侧面 $BCC_1B_1$ 所成角的正切值的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac{3\sqrt 5}{10},\dfrac 54\right)$
【解析】
不妨设正方体的棱长为 $2$．
如图，将正方体 $ABCD-A_1B_1C_1D_1$ 依次按对应的顺序对称，最后得到正方体 $A'B'C'D'-A_1'B_1'C_1'D_1'$．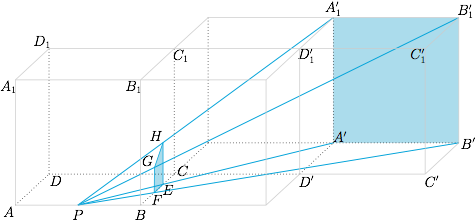
分别连接 $PA'$，$PB'$，$PB_1'$，$PA_1'$，与侧面 $BCC_1B_1$ 依次交于 $E,F,G,H$，则 $Q$ 点是四边形 $EFGH$ 内部（不包含边界）的一点，所求正切值\[\tan\theta=\dfrac{PB}{BQ}=\dfrac{1}{BQ}.\]利用相似三角形，可得\[BF=\dfrac 45,BE=\dfrac 43,FG=\dfrac 25,EH=\dfrac 23,\]于是 $BQ$ 满足\[\dfrac 45=BF<BQ<BH=\sqrt{BE^2+EH^2}=\dfrac{2\sqrt 5}3,\]因此所求正切值的取值范围是 $\left(\dfrac{3\sqrt 5}{10},\dfrac 54\right)$．
如图，将正方体 $ABCD-A_1B_1C_1D_1$ 依次按对应的顺序对称，最后得到正方体 $A'B'C'D'-A_1'B_1'C_1'D_1'$．
分别连接 $PA'$，$PB'$，$PB_1'$，$PA_1'$，与侧面 $BCC_1B_1$ 依次交于 $E,F,G,H$，则 $Q$ 点是四边形 $EFGH$ 内部（不包含边界）的一点，所求正切值\[\tan\theta=\dfrac{PB}{BQ}=\dfrac{1}{BQ}.\]利用相似三角形，可得\[BF=\dfrac 45,BE=\dfrac 43,FG=\dfrac 25,EH=\dfrac 23,\]于是 $BQ$ 满足\[\dfrac 45=BF<BQ<BH=\sqrt{BE^2+EH^2}=\dfrac{2\sqrt 5}3,\]因此所求正切值的取值范围是 $\left(\dfrac{3\sqrt 5}{10},\dfrac 54\right)$．
答案
解析
备注
