想象把一个半径为 $1$ 的单位球放进另一个半径为 $r$（$r>0$）的大球中滚动，那么大球内壁中的任何一个点都可以被小球碾压，也就是对球体而言，表面（面积为 $S=4\pi r^2$）上安全的区域面积 $P$ 为 $0$，于是我们说半径为 $r$ 的球的安全系数$$\lambda (r)=\dfrac {P}{S}=0.$$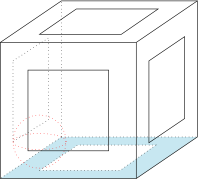
而棱长为 $a$ 的正方体安全系数会好一些，为$$\lambda (a)=4\cdot\dfrac{a-1}{a^2},a>2,$$现在的问题是，相同表面积的正方体和正四面体，哪个安全系数高一些？
而棱长为 $a$ 的正方体安全系数会好一些，为$$\lambda (a)=4\cdot\dfrac{a-1}{a^2},a>2,$$现在的问题是，相同表面积的正方体和正四面体，哪个安全系数高一些？【难度】
【出处】
无
【标注】
【答案】
正四面体高
【解析】
和处理正方体的方式类似，正四面体的情形每个面的安全区域如图所示：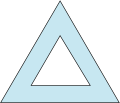
难点在于确定安全区域的宽度．为此，作单位球的外切正四面体，那么切点到其所在的面的任意一边的距离即安全区域的宽度．
用体积法可以求得单位球的外切正四面体的棱长为 $2\sqrt 6$，于是安全区域的宽度为 $\sqrt 2$，进而可得危险区域与整个区域的相似比为$$\left(\dfrac{\sqrt 3}2a-3\sqrt 2\right):\dfrac{\sqrt 3}2a=\left(a-2\sqrt 6\right):a,$$于是安全系数为$$f(a)=1-\left(\dfrac{a-2\sqrt 6}a\right)^2=4\sqrt 6\cdot\dfrac{a-\sqrt 6}{a^2},$$其中 $a\geqslant 2\sqrt 6$．下图为正方体（$f(a)$）和正四面体（$g(a)$）的安全系数与棱长的函数关系图．
事实上，直接比较二者的安全系数可知，正四面体的安全系数高于正方体．这也和我们的感觉保持一致，地震的时候果然应该躲在狭窄的空间比较安全啊！
难点在于确定安全区域的宽度．为此，作单位球的外切正四面体，那么切点到其所在的面的任意一边的距离即安全区域的宽度．用体积法可以求得单位球的外切正四面体的棱长为 $2\sqrt 6$，于是安全区域的宽度为 $\sqrt 2$，进而可得危险区域与整个区域的相似比为$$\left(\dfrac{\sqrt 3}2a-3\sqrt 2\right):\dfrac{\sqrt 3}2a=\left(a-2\sqrt 6\right):a,$$于是安全系数为$$f(a)=1-\left(\dfrac{a-2\sqrt 6}a\right)^2=4\sqrt 6\cdot\dfrac{a-\sqrt 6}{a^2},$$其中 $a\geqslant 2\sqrt 6$．下图为正方体（$f(a)$）和正四面体（$g(a)$）的安全系数与棱长的函数关系图．事实上，直接比较二者的安全系数可知，正四面体的安全系数高于正方体．这也和我们的感觉保持一致，地震的时候果然应该躲在狭窄的空间比较安全啊！
答案
解析
备注
