已知椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$，$F_1,F_2$ 是椭圆的左、右焦点，$A,C$ 是椭圆上关于 $x$ 轴对称的两点，$B$ 点为短轴的端点，线段 $AB$ 恰过右焦点，如图，有 $AB\perp CF_1$，求椭圆的离心率．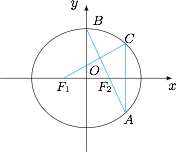
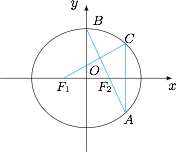
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {\sqrt 5}{5}$
【解析】
连接 $BF_1,AF_1$，易知下图中加“$\cdot$”的角都相等，设为 $\theta$，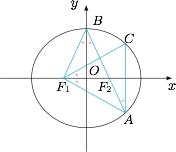
易证$$\angle AF_1B=90^\circ.$$设 $AF_2=x$，则$$AF_1=2a-x,$$在 $\mathrm{Rt}\triangle ABF_1$ 中，有$$(2a-x)^2+a^2=(a+x)^2,$$解得$$x=\dfrac {2a}{3}.$$于是$$\cos{2\theta}=\dfrac {a}{a+x}=\dfrac 35,$$即$$1-2\sin^2\theta=\dfrac 35,$$解得$$\sin\theta =\dfrac {\sqrt 5}{5}.$$从而椭圆的离心率$$e=\dfrac ca=\sin\theta=\dfrac {\sqrt 5}{5}.$$
易证$$\angle AF_1B=90^\circ.$$设 $AF_2=x$，则$$AF_1=2a-x,$$在 $\mathrm{Rt}\triangle ABF_1$ 中，有$$(2a-x)^2+a^2=(a+x)^2,$$解得$$x=\dfrac {2a}{3}.$$于是$$\cos{2\theta}=\dfrac {a}{a+x}=\dfrac 35,$$即$$1-2\sin^2\theta=\dfrac 35,$$解得$$\sin\theta =\dfrac {\sqrt 5}{5}.$$从而椭圆的离心率$$e=\dfrac ca=\sin\theta=\dfrac {\sqrt 5}{5}.$$
答案
解析
备注
