将一堆小球（数量不小于 $2$）分为两堆，记录两堆所包含的小球数之积，将这种操作称为“分堆”，将得到的积称为“分堆积”．将一堆包含 $n$ 个小球的小球进行一次“分堆”，对应的“分堆积”设为 $p_1$；从得到的两堆小球中选出一堆进行“分堆”，对应的“分堆积”设为 $p_2$；再从得到的三堆小球中选出一堆进行“分堆”，对应的“分堆积”设为 $p_3$；依次进行下去，直到最后得到 $n$ 堆小球（每堆的小球数量均为 $1$）为止．设$$S(n)=p_1+p_2+\cdots +p_{n-1},$$证明：$S(n)$ 是一个与分堆的具体过程无关的定值．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设第一次分堆将 $n$ 个小球分成 $a_1$ 和 $a_2$ 两个部分，那么$$n^2=(a_1+a_2)^2=a_1^2+a_2^2+2a_1a_2,$$可以将这个等式看作 $n^2$“分裂”为了 $a_1^2$ 和 $a_2^2$，与此同时产生“余项”$2a_1a_2$，也即 $2p_1$．随着“分裂”的持续进行直至最终的 $n$ 个 $1^2$，所产生的“余项”之和为$$2p_1+2p_2+\cdots 2p_{n-1}=2S(n),$$因此我们有$$n^2=\underbrace{1^2+1^2+\cdots +1^2}_{n}+2S(n),$$即$$S(n)=\dfrac 12n(n-1).$$这个方法有一个优美的几何解释：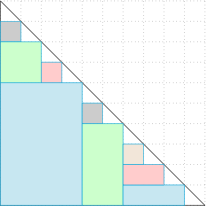
如图，所有矩形的面积之和即 $S(n)$．
如图，所有矩形的面积之和即 $S(n)$．
答案
解析
备注
