已知函数 $f(x)=\begin{cases}
\dfrac{1}{2}x+\dfrac{3}{2},x\leqslant 1\\
\ln x,x>1\\
\end{cases}$（$\ln x$ 是以 $e$ 为底的自然对数，$e=2.71828\cdots$），若存在实数 $m,n(m<n)$，满足 $f(m)=f(n)$，则 $n-m$ 的取值范围为 \((\qquad)\) ．
\dfrac{1}{2}x+\dfrac{3}{2},x\leqslant 1\\
\ln x,x>1\\
\end{cases}$（$\ln x$ 是以 $e$ 为底的自然对数，$e=2.71828\cdots$），若存在实数 $m,n(m<n)$，满足 $f(m)=f(n)$，则 $n-m$ 的取值范围为 \((\qquad)\) ．
【难度】
【出处】
2018年全国高中数学联赛黑龙江省预赛
【标注】
【答案】
C
【解析】
根据题意，作出函数 $f(x)=\begin{cases}
\dfrac{1}{2}x+\dfrac{3}{2},x\leqslant 1\\
\ln x,x>1\\
\end{cases}$ 的图像如图所示．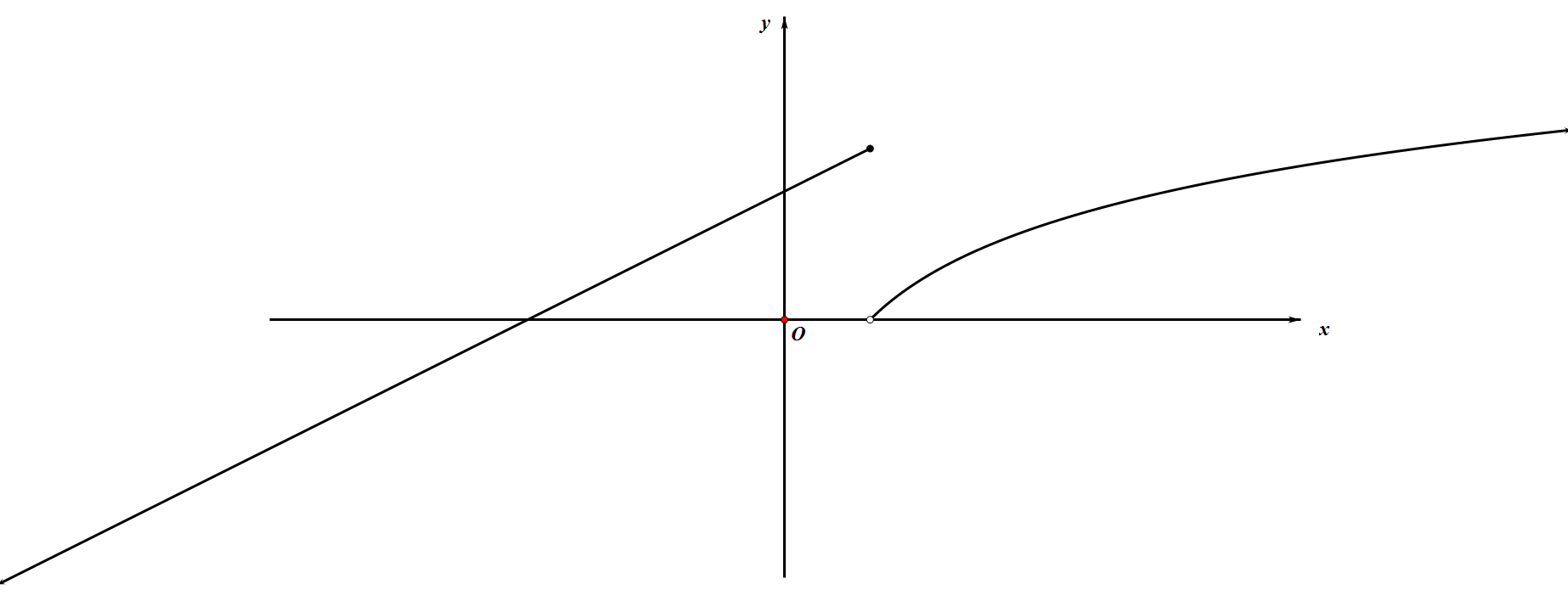
因为存在实数 $m,n(m<n)$，满足 $f(m)=f(n)$，所以根据函数图像可得 $-3<m\leqslant 1,1<n\leqslant e^2$．所以有 $\dfrac{1}{2}m+\dfrac{3}{2}=\ln n$，即 $m=2\ln n-3$．故有 $n-m=n-2\ln n+3$．令 $g(x)=x-2\ln x+3,x\in(1,e^2]$，则有 $g^\prime (x)=1-\dfrac{2}{x}=\dfrac{x-2}{x}$．当 $1<x<2$ 时，$g^\prime(x)<0$，即 $g(x)$ 在 $(1,2)$ 上为减函数；当 $2<x\leqslant e^2$ 时，$g^\prime(x)>0$，即 $g(x)$ 在 $(2,e^2]$ 上为增函数．所以 $g(x)_{min}=g(2)=5-2\ln 2$．又 $g(e^2)=e^2-1>g(1)=4$，所以 $g(x)\in[5-2\ln 2,e^2-1]$，所以 $n-m$ 的取值范围是 $[5-2\ln 2,e^2-1]$，故选 $C$．
\dfrac{1}{2}x+\dfrac{3}{2},x\leqslant 1\\
\ln x,x>1\\
\end{cases}$ 的图像如图所示．
因为存在实数 $m,n(m<n)$，满足 $f(m)=f(n)$，所以根据函数图像可得 $-3<m\leqslant 1,1<n\leqslant e^2$．所以有 $\dfrac{1}{2}m+\dfrac{3}{2}=\ln n$，即 $m=2\ln n-3$．故有 $n-m=n-2\ln n+3$．令 $g(x)=x-2\ln x+3,x\in(1,e^2]$，则有 $g^\prime (x)=1-\dfrac{2}{x}=\dfrac{x-2}{x}$．当 $1<x<2$ 时，$g^\prime(x)<0$，即 $g(x)$ 在 $(1,2)$ 上为减函数；当 $2<x\leqslant e^2$ 时，$g^\prime(x)>0$，即 $g(x)$ 在 $(2,e^2]$ 上为增函数．所以 $g(x)_{min}=g(2)=5-2\ln 2$．又 $g(e^2)=e^2-1>g(1)=4$，所以 $g(x)\in[5-2\ln 2,e^2-1]$，所以 $n-m$ 的取值范围是 $[5-2\ln 2,e^2-1]$，故选 $C$．
题目
答案
解析
备注
