已知在△ $ABC$ 中，$\angle A$，$\angle B$，$\angle C$ 的对边分别为 $a$，$b$，$c$，解决下列问题：
【难度】
【出处】
无
【标注】
-
若 $\angle A=2\angle B$，求证：${{a}^{2}}=b\left( b+c \right)$．标注答案略解析
方法不唯一，
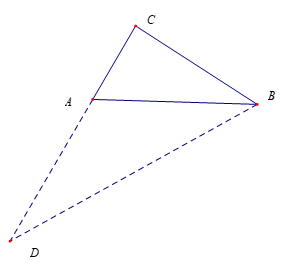
延长 $CA$ 到 $D$，使得 $AD=AB=c$，$CD=CA+AD=b+c$
得到 $\angle D=\angle ABD$，
于是 $\angle CAB=2\angle D$，由已知 $\angleCAB=2\angle CBA$
∴ $\angle CDB=\angle CBA$，又 $\angleC=\angle C$
∴△ $CAB$ ∽△ $CBD$，
∴ $\dfrac{CA}{CB}=\dfrac{CB}{CD}$，即 $C{{B}^{2}}=CA\cdot CD$
即 ${{a}^{2}}=b\left(b+c \right)$ ……5分 -
计算 $\cos {{72}^{\circ }}$．标注答案略解析
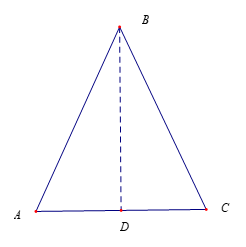方法不唯一，构造△ $ABC$，使得 $\angle A=\angle C={{72}^{\circ }}$，$\angleB={{36}^{\circ }}$，
取 $AC$ 中点 $D$，连结 $BD$，则 $\cos{{72}^{\circ }}=\dfrac{AD}{AB}=\dfrac{AC}{2AB}=\dfrac{b}{2c}$，
由（1）可知 ${{a}^{2}}=b\left( b+c \right)$，结合 $a=c$，
得到 ${{c}^{2}}-bc-{{b}^{2}}=0$，即 ${{\left( \dfrac{b}{c} \right)}^{2}}+\left( \dfrac{b}{c}\right)-1=0$，
解得 $\dfrac{b}{c}=\dfrac{-1+\sqrt{5}}{2}$（$\dfrac{b}{c}=\dfrac{-1-\sqrt{5}}{2}<0$ 舍掉）
于是 $\cos{{72}^{\circ }}=\dfrac{b}{2c}=\dfrac{\sqrt{5}-1}{4}$．……10分
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
