过圆 $O$ 外一点 $P$，做两条切线 $PA$，$PB$，切点分别为 $A,B$，过 $P$ 的割线 $PCD$ 交圆于 $CD$ 两点，其中 $C$ 在线段 $PD$ 上，连结 $CD$ 的中点 $M$ 与 $A$，并延长 $AM$ 交圆 $O$ 于 $E$，求证：$BE$ ∥ $PD$．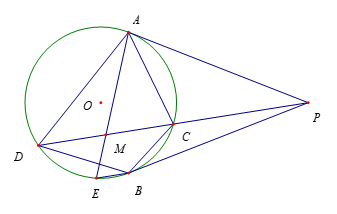
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
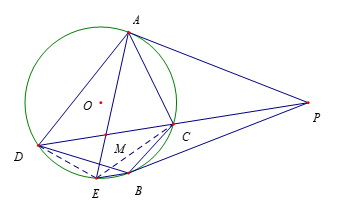答案不唯一，连结 $DE$，$EC$，
∵ $PA$ 切圆 $O$ 于 $A$，
∴ $\angle PAC=\angle PDA$（弦切角等于夹弧所对圆周角），结合 $\angle APC=\angle DPA$，
∴△ $PAC$ ∽△ $PDA$
∴ $\dfrac{AC}{DA}=\dfrac{PA}{PD}$，同理可 $\dfrac{BC}{DB}=\dfrac{PB}{PD}$，结合切线长定理 $PA=PB$
∴ $\dfrac{AC}{AD}=\dfrac{BC}{BD}$，……3分
根据同弧所对圆周角相等可得 $\angle MAD=\angle MCE$，$\angle MDA=\angle MEC$，
∴△ $MAD$ ∽ $MCE$
∴ $\dfrac{EC}{DA}=\dfrac{CM}{MA}$，同理可证△ $MAC$ ∽△ $MDE$，进而 $\dfrac{ED}{CA}=\dfrac{MD}{MA}$，
根据已知 $MC=MD$，得到 $\dfrac{EC}{DA}=\dfrac{ED}{CA}$ ……6分
∴ $\dfrac{DE}{CE}=\dfrac{AC}{AD}$
∴ $\dfrac{DE}{CE}=\dfrac{BC}{BD}$，即 $\dfrac{CE}{DB}=\dfrac{DE}{CB}$，结合 $\angle DEC=\angle CBD$
∴△ $DEC$ ∽△ $CBD$
∴ $\angle DCE=\angle CDB$
∴弧 $DE$ $=$ 弧 $BC$
∴ $BE$ ∥ $CD$ ……10分
答案
解析
备注
