在棱长为 $1$ 的正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中,$E$、$F$、$G$ 点分别为 $A{A_1}$、$AD$、${A_1}{B_1}$ 的中点,求:
【难度】
【出处】
2005年复旦大学保送生招生测试
【标注】
-
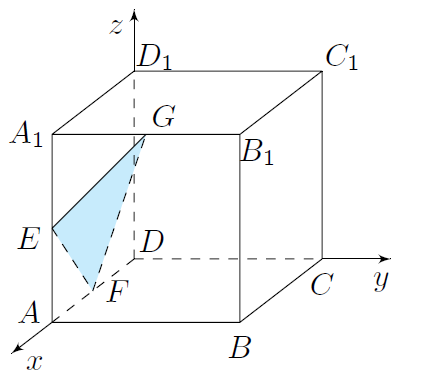
点 $B$ 到平面 $EFG$ 的距离;标注答案$\dfrac{\sqrt 3}2$解析如图建系,$A\left( {1,0,0} \right)$,$B\left( {1,1,0} \right)$,$C\left( {0,1,0} \right)$,$D\left( {0,0,0} \right)$,${A_1}\left( {1,0, 1} \right)$,${B_1}\left( {1,1,1} \right)$,${C_1}\left( {0,1,1} \right)$,${D_1}\left( {0,0,1} \right)$,$E\left( {1,0,\dfrac{1}{2}} \right)$,$F\left( {\dfrac{1}{2},0,0} \right)$,$G\left( {1,\dfrac{1}{2},1} \right)$.
 于是$$\begin{split}\overrightarrow {EF} &= \left( { - \dfrac{1}{2},0, - \dfrac{1}{2}} \right),\\\overrightarrow {EG} &= \left( {0,\dfrac{1}{2},\dfrac{1}{2}} \right),\end{split}$$因此平面 $EFG$ 的法向量为 $\overrightarrow {{n}} = \left( { - 1, - 1,1} \right)$.
于是$$\begin{split}\overrightarrow {EF} &= \left( { - \dfrac{1}{2},0, - \dfrac{1}{2}} \right),\\\overrightarrow {EG} &= \left( {0,\dfrac{1}{2},\dfrac{1}{2}} \right),\end{split}$$因此平面 $EFG$ 的法向量为 $\overrightarrow {{n}} = \left( { - 1, - 1,1} \right)$.
所以 $\overrightarrow {BE} $ 在 $\overrightarrow {{n}} $ 上的投影为$$\dfrac{{\left| {\left( {0, - 1,\dfrac{1}{2}} \right) \cdot \left( { - 1, - 1,1} \right)} \right|}}{{\sqrt 3 }} = \dfrac{{\sqrt 3 }}{2}.$$ -
二面角 $G - EF - {D_1}$ 的平面角 $\theta $ 的大小.标注答案$\arccos\dfrac{\sqrt 3}3$解析因为平面 $EF{D_1}$ 的法向量为 $\left( {0,1,0} \right)$,所以$$\cos \theta = \left| {\dfrac{{\left( {0,1,0} \right)\cdot\left( { - 1, - 1,1} \right)}}{{\sqrt 3 }}} \right| = \dfrac{{\sqrt 3 }}{3},$$故 $\theta=\arccos\dfrac{\sqrt 3}3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2