略

设椭圆的方程为 $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\left(a>b>0 \right)$，设外切菱形面积最小值为 $m$
先求出外切平行四边形面积最小值 ${m}'$，容易得到 $m\geqslant {m}'$，
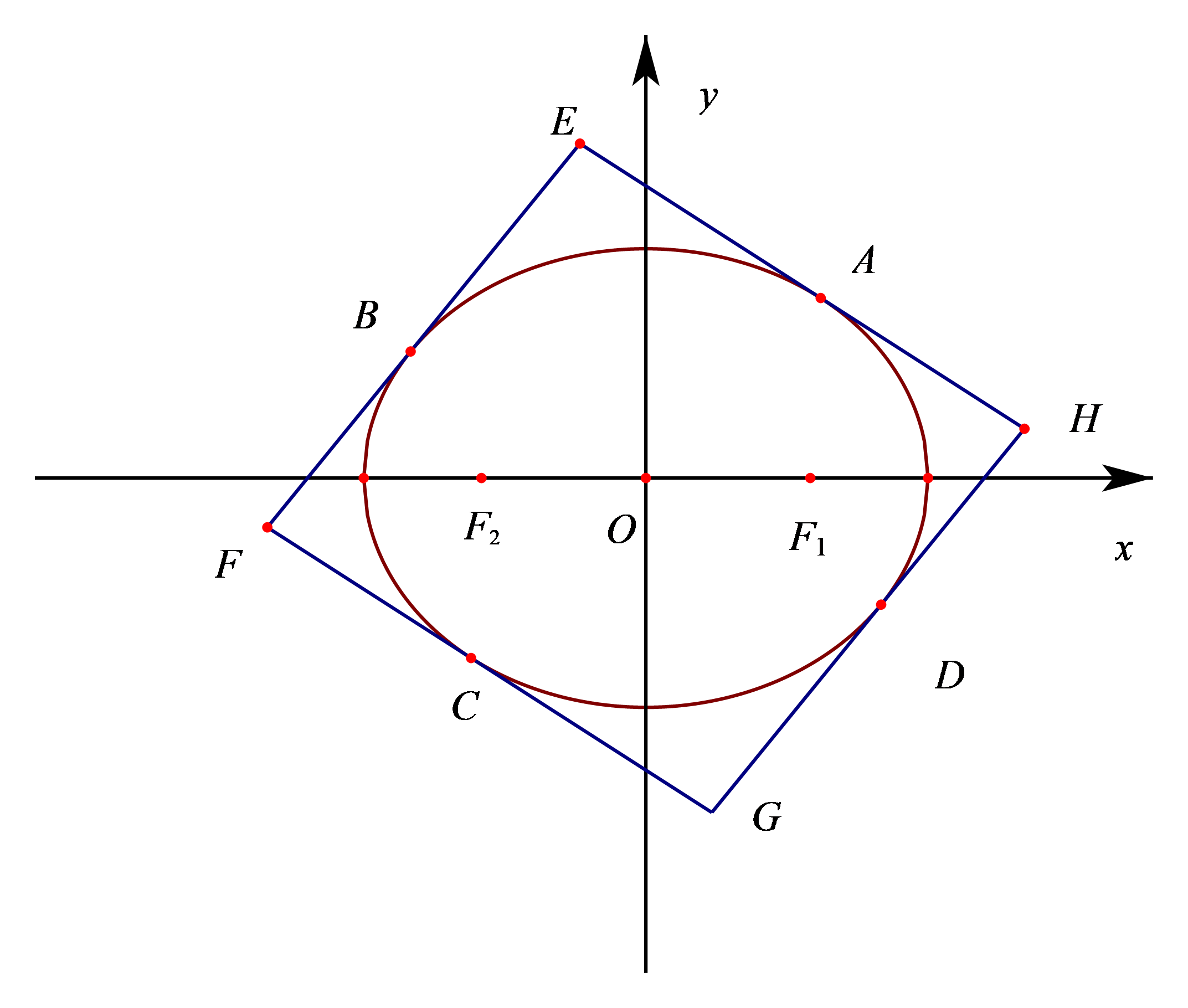
如图，设 $A\left( a\cos \alpha ,b\sin \alpha \right)$，$B\left( a\cos \beta ,b\sin \beta \right)$，（$0\leqslant\alpha <\dfrac{\mathrm{ }\!\!\pi\!\!\text{ }}{2}\leqslant \beta <\mathrm{}\!\!\pi\!\!\text{ }$）
则 $EH:\dfrac{x\cos \alpha }{a}+\dfrac{y\sin \alpha }{b}=1$，$FG:\dfrac{x\cos \alpha }{a}+\dfrac{y\sin \alpha }{b}=-1$
$EF:\dfrac{x\cos \beta }{a}+\dfrac{y\sin\beta }{b}=1$，$GH:\dfrac{x\cos \beta }{a}+\dfrac{y\sin \beta}{b}=-1$
计算得到 $E\left( \dfrac{a\left( \sin \alpha -sin\beta \right)}{\sin \left( \alpha -\beta \right)},-\dfrac{b\left( \cos \alpha -\cos\beta \right)}{\sin \left( \alpha-\beta \right)} \right)$，$H\left( -\dfrac{a\left( \sin \alpha +sin\beta \right)}{\sin \left( \alpha -\beta \right)},\dfrac{b\left( \cos \alpha +\cos\beta \right)}{\sin \left( \alpha-\beta \right)} \right)$
则 $S=2\left| \overrightarrow{OE}\times \overrightarrow{OH}\right|=4ab\left| \dfrac{1}{\sin \left( \alpha -\beta \right)} \right|\geqslant 4ab$（$\sin \left( \alpha -\beta \right)=-1$），得到 ${m}'=4ab$
若 $\overrightarrow{OE}\cdot \overrightarrow{OH}=0$，即 ${{a}^{2}}{{\sin }^{2}}\alpha +{{b}^{2}}{{\cos }^{2}}\alpha={{a}^{2}}{{\sin }^{2}}\beta +{{b}^{2}}{{\cos }^{2}}\beta $，即 ${{\sin }^{2}}\alpha ={{\sin }^{2}}\beta $
结合 $\sin \left( \alpha -\beta \right)=-1$
只能 $\alpha =\dfrac{\mathrm{ }\!\!\pi\!\!\text{ }}{4}$，$\beta =\dfrac{3\mathrm{ }\!\!\pi\!\!\text{ }}{4}$，故 $m=4ab$，此时菱形四个点为 $\left( \pm \sqrt{2}a,0\right)$，$\left( 0,\pm \sqrt{2}b \right)$

略

尺规做出 $\left( \pm \sqrt{2}a,0 \right)$，$\left(0,\pm \sqrt{2}b \right)$ 基本操作．