已知 $y=f\left( x \right)$，$x\in \left[ a,b \right]$，关于 $x$ 轴旋转一周所形成的旋转体的体积和侧面积公式如下：
$V=\pi \int_{a}^{b}{{{\left[ f\left( x \right) \right]}^{2}}dx}$，
${{S}_{}}=2\pi \int_{a}^{b}{f\left( x \right)\sqrt{1+{{\left[ {f}'\left( x \right) \right]}^{2}}}}dx$
请利用上述公式，
$V=\pi \int_{a}^{b}{{{\left[ f\left( x \right) \right]}^{2}}dx}$，
${{S}_{}}=2\pi \int_{a}^{b}{f\left( x \right)\sqrt{1+{{\left[ {f}'\left( x \right) \right]}^{2}}}}dx$
请利用上述公式，
【难度】
【出处】
无
【标注】
-
用积分方式解释球的表面积和体积；标注答案略解析略
-
如图，求出内径为 $R-r$，外径为 $R+r$ 的游泳圈表面积和体积．
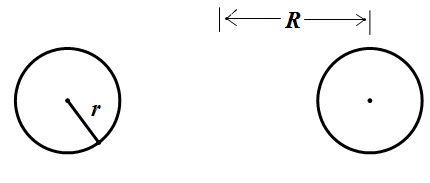标注答案$S=4{{\pi}^{2}}Rr$，$V=2{{\pi}^{2}}R{{r}^{2}}$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
