$xy$ 平面上的一个椭圆，焦点在 $\left( 9 ,20 \right)$ 和 $\left( 49 ,55 \right)$ 并与 $x$ 轴相切，求长轴的长度．
【难度】
【出处】
1985年第3届美国数学邀请赛（AIME）
【标注】
【答案】
85
【解析】
椭圆焦点分别为 ${{F}_{1}}\left( 9 ,20 \right)$ 及 ${{F}_{2}}\left( 49, 55 \right)$，${{F}_{2}}$ 关于 $x$ 轴的对称点为 ${{F}_{2}}^{\prime }\left( 49 ,-55 \right)$，我们说明：椭圆的长轴 $k$ 等于线段 ${{F}_{1}}{{F}_{2}}^{\prime}$ 的长度，用两点间的距离公式易得 $k=85$．
为了说明这一点，设 $P$ 是椭圆与 $x$ 轴的切点，线段 ${{F}_{1}}{{F}_{2}}^{\prime}$ 交 $x$ 轴于另一点 ${P}'$（如图所示，该图故意画得不准确）．由三角形不等式可知：
$P{{F}_{1}}+P{{F}_{2}}^{\prime}>{{F}_{1}}{{F}_{2}}^{\prime }={P}'{{F}_{1}}+{P}'{{F}_{2}}^{\prime}={P}'{{F}_{1}}+{P}'{{F}_{2}}$．（9）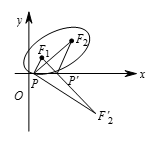
但由椭圆定义，对椭圆上任何点 $Q$ 都有 $Q{{F}_{1}}+Q{{F}_{2}}=k$，特别有 $P{{F}_{1}}+P{{F}_{2}}=k$．（10）
此外对椭圆外的任一点 $Q$，都应有 $Q{{F}_{1}}+Q{{F}_{2}}>k$．由切线的定义，${P}'$ 应在椭圆外，所以
${P}'{{F}_{1}}+{P}'{{F}_{2}}>k$．（11）
由（10）及（11）知 ${P}'{{F}_{1}}+P{{F}_{2}}^{\prime }=P{{F}_{1}}+P{{F}_{2}}<{P}'{{F}_{1}}+{P}'{{F}_{2}}$，
与（9）矛盾．这个矛盾推翻了关于 $P$ 与 ${P}'$ 是不同点的假设，故 $P$ 与 ${P}'$ 重合，这就是所要证明的．
为了说明这一点，设 $P$ 是椭圆与 $x$ 轴的切点，线段 ${{F}_{1}}{{F}_{2}}^{\prime}$ 交 $x$ 轴于另一点 ${P}'$（如图所示，该图故意画得不准确）．由三角形不等式可知：
$P{{F}_{1}}+P{{F}_{2}}^{\prime}>{{F}_{1}}{{F}_{2}}^{\prime }={P}'{{F}_{1}}+{P}'{{F}_{2}}^{\prime}={P}'{{F}_{1}}+{P}'{{F}_{2}}$．（9）
但由椭圆定义，对椭圆上任何点 $Q$ 都有 $Q{{F}_{1}}+Q{{F}_{2}}=k$，特别有 $P{{F}_{1}}+P{{F}_{2}}=k$．（10）此外对椭圆外的任一点 $Q$，都应有 $Q{{F}_{1}}+Q{{F}_{2}}>k$．由切线的定义，${P}'$ 应在椭圆外，所以
${P}'{{F}_{1}}+{P}'{{F}_{2}}>k$．（11）
由（10）及（11）知 ${P}'{{F}_{1}}+P{{F}_{2}}^{\prime }=P{{F}_{1}}+P{{F}_{2}}<{P}'{{F}_{1}}+{P}'{{F}_{2}}$，
与（9）矛盾．这个矛盾推翻了关于 $P$ 与 ${P}'$ 是不同点的假设，故 $P$ 与 ${P}'$ 重合，这就是所要证明的．
答案
解析
备注
