一个机器零件的形状是一个有缺口的圆,如图所示,这个圆的半径是 $\sqrt{50}$,$AB$ 的长度是6,$BC$ 的长度是2,$\angle ABC$ 是直角.求点 $B$ 与圆心的距离的平方.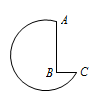

【难度】
【出处】
1983年第1届美国数学邀请赛(AIME)
【标注】
【答案】
26
【解析】
如图所示,补成一个圆 $O$,连接 $AC$,则由勾股定理得 $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{6}^{2}}+{{2}^{2}}}=\sqrt{40}$,
$\sin \angle BAC=\frac{2}{\sqrt{40}}=\frac{1}{\sqrt{10}}$.
设 $AC$ 的中点为 $D$,连接 $OA$,$OD$,则 $\angle ODA=90{}^\circ $,
$\cos \angle OAD=\frac{\frac{\sqrt{40}}{2}}{\sqrt{50}}=\frac{1}{\sqrt{5}}$.
由三角计算易知 $\cos \angle OAB=\cos \left( \angle OAD-\angle BAC \right)=\frac{\sqrt{2}}{2}$.
在 $\triangle OAB$ 中,由余弦定理得
$O{{B}^{2}}=O{{A}^{2}}+A{{B}^{2}}-2OA\cdot AB\cos\angle OAB$
$={{\sqrt{50}}^{2}}+{{6}^{2}}-2\sqrt{50}\times6\times \frac{\sqrt{2}}{2}$
$=26$.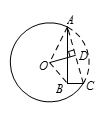
$\sin \angle BAC=\frac{2}{\sqrt{40}}=\frac{1}{\sqrt{10}}$.
设 $AC$ 的中点为 $D$,连接 $OA$,$OD$,则 $\angle ODA=90{}^\circ $,
$\cos \angle OAD=\frac{\frac{\sqrt{40}}{2}}{\sqrt{50}}=\frac{1}{\sqrt{5}}$.
由三角计算易知 $\cos \angle OAB=\cos \left( \angle OAD-\angle BAC \right)=\frac{\sqrt{2}}{2}$.
在 $\triangle OAB$ 中,由余弦定理得
$O{{B}^{2}}=O{{A}^{2}}+A{{B}^{2}}-2OA\cdot AB\cos\angle OAB$
$={{\sqrt{50}}^{2}}+{{6}^{2}}-2\sqrt{50}\times6\times \frac{\sqrt{2}}{2}$
$=26$.

答案
解析
备注