图中的多面体的底面是边长为 $s$ 的正方形，上面的棱平行于底面，其长为 $2s$，其余的棱长都是 $s$，已知 $s=6\sqrt{2}$，求这个多面体的体积．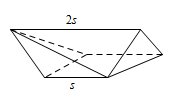
【难度】
【出处】
1983年第1届美国数学邀请赛（AIME）
【标注】
【答案】
288
【解析】
考虑图中的棱长为 $2s$ 的正四面体，连接 $AC$，$BC$，$AD$，$BD$ 的中点．这样做成的四边形是个正方形（为什么），这个四边形所在的平面把正四面体分为两个与本题中的多面体全等的多面体，于是我们只需求出正四面体的体积再除以 $2$ 就行了．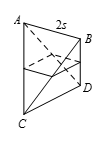
因为正四面体的棱为 $2s$，所以
${{V}_{ABCD}}=\frac{1}{3}{{S}_{}}h=\frac{1}{3}\times\frac{\sqrt{3}}{4}{{\left( 2s \right)}^{2}}\times \sqrt{\frac{2}{3}}\left( 2s\right)=\frac{2}{3}\sqrt{2}{{s}^{3}}$
因此，所求多面体的体积是
$V=\frac{1}{2}{{V}_{ABCD}}=\frac{\sqrt{2}}{3}\times {{\left(6\sqrt{2} \right)}^{3}}=288$．
因为正四面体的棱为 $2s$，所以${{V}_{ABCD}}=\frac{1}{3}{{S}_{}}h=\frac{1}{3}\times\frac{\sqrt{3}}{4}{{\left( 2s \right)}^{2}}\times \sqrt{\frac{2}{3}}\left( 2s\right)=\frac{2}{3}\sqrt{2}{{s}^{3}}$
因此，所求多面体的体积是
$V=\frac{1}{2}{{V}_{ABCD}}=\frac{\sqrt{2}}{3}\times {{\left(6\sqrt{2} \right)}^{3}}=288$．
答案
解析
备注
