一个圆的直径 $AB$ 的长度是两位的整数（十进制）．把两个数字颠倒一下，就是与直径 $AB$ 垂直的弦 $CD$ 的长度，如图所示．从交点 $H$ 到圆心 $O$ 的距离是一个正有理数，求 $AB$ 的长度．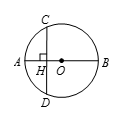
【难度】
【出处】
1983年第1届美国数学邀请赛（AIME）
【标注】
【答案】
65
【解析】
如图所示，令 $AB=10t+u$．$u t$ 都是从0到9的自然数，则 $CD=10u+t$．我们来求 $t$ 和 $u$ 使 $OH$ 是一个正的有理数．显然，$t\geqslant u$，为了保证 $OH$ 是正的，我们设 $t>u$．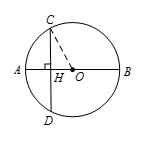
因为 $\vartriangle OCH$ 是直角三角形，我们用勾股定理把 $OH$ 用 $AB$ 和 $CD$ 表示出来：
$OH=\sqrt{{{\left( OC \right)}^{2}}-{{\left( CH \right)}^{2}}}$
$=\frac{1}{2}\sqrt{{{\left(10t+u \right)}^{2}}-{{\left( 10u+t \right)}^{2}}}$
$=\frac{3}{2}\sqrt{11\left({{t}^{2}}-{{u}^{2}} \right)}$，
所以，要使 $OH$ 是有理数，当且仅当 $\sqrt{11\left({{t}^{2}}-{{u}^{2}} \right)}$ 是有理数，要使整数的平方根是有理数，这个平方根必须是整数，而只有能被开尽的整数的平方根是有理数，这样一来，我们就应求 $t$ 和 $u$ 使 $11\left( {{t}^{2}}-{{u}^{2}} \right)$ 是完全平方数，这就是必须存在一个正整数 $m$，使 ${{t}^{2}}-{{u}^{2}}=11{{m}^{2}}$，$\left( t-u\right)\left( t+u \right)=11{{m}^{2}}$．11不可能整除 $t-u$（为什么？），因此，它必须整除 $t+u$，因此只可能 $t+u=11$（为什么？），所以 $t-u={{m}^{2}}$．于是我们就要找出两个数，和为11，差是完全平方．
最后，考查满足 $t+u=11$ 的所有 $t$ 和 $u$ $\left(t>u \right)$：
$t=9$，$u=2$；$t=8$，$u=3$；
$t=7$，$u=4$；$t=6$，$u=5$．
只有最后一种情况 $t-u$ 是完全平方，所以 $AB=65$．
因为 $\vartriangle OCH$ 是直角三角形，我们用勾股定理把 $OH$ 用 $AB$ 和 $CD$ 表示出来：$OH=\sqrt{{{\left( OC \right)}^{2}}-{{\left( CH \right)}^{2}}}$
$=\frac{1}{2}\sqrt{{{\left(10t+u \right)}^{2}}-{{\left( 10u+t \right)}^{2}}}$
$=\frac{3}{2}\sqrt{11\left({{t}^{2}}-{{u}^{2}} \right)}$，
所以，要使 $OH$ 是有理数，当且仅当 $\sqrt{11\left({{t}^{2}}-{{u}^{2}} \right)}$ 是有理数，要使整数的平方根是有理数，这个平方根必须是整数，而只有能被开尽的整数的平方根是有理数，这样一来，我们就应求 $t$ 和 $u$ 使 $11\left( {{t}^{2}}-{{u}^{2}} \right)$ 是完全平方数，这就是必须存在一个正整数 $m$，使 ${{t}^{2}}-{{u}^{2}}=11{{m}^{2}}$，$\left( t-u\right)\left( t+u \right)=11{{m}^{2}}$．11不可能整除 $t-u$（为什么？），因此，它必须整除 $t+u$，因此只可能 $t+u=11$（为什么？），所以 $t-u={{m}^{2}}$．于是我们就要找出两个数，和为11，差是完全平方．
最后，考查满足 $t+u=11$ 的所有 $t$ 和 $u$ $\left(t>u \right)$：
$t=9$，$u=2$；$t=8$，$u=3$；
$t=7$，$u=4$；$t=6$，$u=5$．
只有最后一种情况 $t-u$ 是完全平方，所以 $AB=65$．
答案
解析
备注
