图1-4中两圆的半径为8和6，两个圆心的距离是12，过两圆交点之一的直线被两圆截出相等的弦 $QP$ 和 $PR$，求 $QP$ 长度的平方．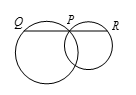
【难度】
【出处】
1983年第1届美国数学邀请赛（AIME）
【标注】
【答案】
130
【解析】
如图所示，对有阴影的三角形用勾股定理，得到 ${{\left( 2a \right)}^{2}}+{{\left( b-c \right)}^{2}}={{12}^{2}}$．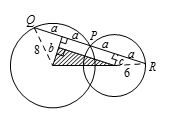
但是 $b=\sqrt{64-{{a}^{2}}}$，$c=\sqrt{36-{{a}^{2}}}$，所以 $4{{a}^{2}}+{{\left(\sqrt{64-{{a}^{2}}}-\sqrt{36-{{a}^{2}}} \right)}^{2}}=144$．
化简，得到 ${{a}^{2}}-22=\sqrt{\left(64-{{a}^{2}} \right)\left( 36-{{a}^{2}} \right)}$，
平方再化简，得到 $4{{a}^{2}}=130$．于是 ${{\left(2a \right)}^{2}}=4{{a}^{2}}=130$．
但是 $b=\sqrt{64-{{a}^{2}}}$，$c=\sqrt{36-{{a}^{2}}}$，所以 $4{{a}^{2}}+{{\left(\sqrt{64-{{a}^{2}}}-\sqrt{36-{{a}^{2}}} \right)}^{2}}=144$．化简，得到 ${{a}^{2}}-22=\sqrt{\left(64-{{a}^{2}} \right)\left( 36-{{a}^{2}} \right)}$，
平方再化简，得到 $4{{a}^{2}}=130$．于是 ${{\left(2a \right)}^{2}}=4{{a}^{2}}=130$．
答案
解析
备注
