如图所示，一个圆的两弦相交，其中 $B$ 在 $\overset\frown{AD}$ 小弧上，设圆半径是5，$BC=6$，$AD$ 被 $BC$ 等分．又设从 $A$ 出发的弦只有 $AD$ 能被 $BC$ 等分，这样可以知道 $AB$ 小弧对应的圆心角的正弦是一个有理数．如果把这个有理数化成既约分数 $\frac{m}{n}$，求 $mn$．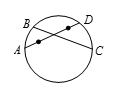
【难度】
【出处】
1983年第1届美国数学邀请赛（AIME）
【标注】
【答案】
175
【解析】
考查从 $A$ 出发的所有的弦（图（a）），这些弦的终点的轨迹是半径为5的已知圆，所以他们的中点的轨迹是（在 $A$ 点）与这个圆内切的半径为 $\frac{5}{2}$ 的圆（只用把已知圆以 $\frac{1}{2}$ 的比例向 $A$ 点收缩就可以）．因此 $BC$ 必须与这个小圆相切，因为如果它与这个小圆交于两点，如图（a）所示，就会有两个从 $A$ 出发的弦被 $BC$ 等分．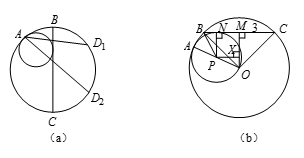
现在再看图（b），其中 $O$，$P$ 是两个圆的圆心，$BC$ 与小圆相切（于 $N$ 点）．我们如下画出辅助线：$OA$（过 $P$ 点），$OB$，$OC$，$MO\bot BC$，$NP\bot BC$，$PX\parallel BC$．我们来求 $\sin \angle BOA$．先求出 $\vartriangle BOP$ 的三个边：
因为 $MC=3$，所以 $MO=\sqrt{{{5}^{2}}-{{3}^{2}}}=4$．
又 $NP=\frac{1}{2}AO=\frac{5}{2}$，$MNPX$ 是个矩形，所以 $MX=\frac{5}{2}$，$OX=\frac{3}{2}$．
因为 $\vartriangle PXO$ 是个直角三角形，$OP=\frac{5}{2}$，$OX=\frac{3}{2}$，所以 $PX=\sqrt{{{\left(\frac{5}{2} \right)}^{2}}-{{\left( \frac{3}{2} \right)}^{2}}}=2$．
又 $MN=2$，所以 $BN=1$．
因为 $\vartriangle BNP$ 是直角三角形，所以 $B{{P}^{2}}=1+\frac{25}{4}=\frac{29}{4}$．
现在已经求出了 $\Delta BOP$ 的三个边，对 $\theta =\angle BOP$ 用余弦定理，我们得到 $\frac{29}{4}=25+\frac{25}{4}-2\times 5\times \frac{5}{2}\cos \theta$，$\cos \theta =\frac{24}{25}$．所以 $\sin \theta=\sqrt{1-{{\left( \frac{24}{25} \right)}^{2}}}=\frac{7}{25}$．所求的答案是175．
现在再看图（b），其中 $O$，$P$ 是两个圆的圆心，$BC$ 与小圆相切（于 $N$ 点）．我们如下画出辅助线：$OA$（过 $P$ 点），$OB$，$OC$，$MO\bot BC$，$NP\bot BC$，$PX\parallel BC$．我们来求 $\sin \angle BOA$．先求出 $\vartriangle BOP$ 的三个边：因为 $MC=3$，所以 $MO=\sqrt{{{5}^{2}}-{{3}^{2}}}=4$．
又 $NP=\frac{1}{2}AO=\frac{5}{2}$，$MNPX$ 是个矩形，所以 $MX=\frac{5}{2}$，$OX=\frac{3}{2}$．
因为 $\vartriangle PXO$ 是个直角三角形，$OP=\frac{5}{2}$，$OX=\frac{3}{2}$，所以 $PX=\sqrt{{{\left(\frac{5}{2} \right)}^{2}}-{{\left( \frac{3}{2} \right)}^{2}}}=2$．
又 $MN=2$，所以 $BN=1$．
因为 $\vartriangle BNP$ 是直角三角形，所以 $B{{P}^{2}}=1+\frac{25}{4}=\frac{29}{4}$．
现在已经求出了 $\Delta BOP$ 的三个边，对 $\theta =\angle BOP$ 用余弦定理，我们得到 $\frac{29}{4}=25+\frac{25}{4}-2\times 5\times \frac{5}{2}\cos \theta$，$\cos \theta =\frac{24}{25}$．所以 $\sin \theta=\sqrt{1-{{\left( \frac{24}{25} \right)}^{2}}}=\frac{7}{25}$．所求的答案是175．
答案
解析
备注
