如图所示,$P$ 是 $\vartriangle ABC$ 内一点,过 $P$ 分别作直线平行于 $\vartriangle ABC$ 的各边,所形成的小三角形 ${{t}_{1}}$,${{t}_{2}}$ 与 ${{t}_{3}}$ 的面积分别是4,9和49.
求 $\vartriangle ABC$ 的面积.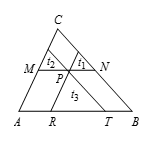
求 $\vartriangle ABC$ 的面积.

【难度】
【出处】
1984年第2届美国数学邀请赛(AIME)
【标注】
【答案】
144
【解析】
设 $MP=p$,$PN=q$,$RT=r$,由于三角形 ${{t}_{1}}$,${{t}_{2}}$,${{t}_{3}}$ 都和 $\vartriangle ABC$ 相似,因此,面积平方根之比等于对应边之比.
设 $AB=c$,$\vartriangle ABC$ 面积为 $S$,则有 $\frac{2}{\sqrt{S}}=\frac{q}{c}$,$\frac{3}{\sqrt{S}}=\frac{p}{c}$,$\frac{7}{\sqrt{S}}=\frac{r}{c}$.
三式相加得 $\frac{2+3+7}{\sqrt{S}}=\frac{p+q+r}{c}=\frac{c}{c}=1$.
所以 $\sqrt{S}=12$,$S=144$.
设 $AB=c$,$\vartriangle ABC$ 面积为 $S$,则有 $\frac{2}{\sqrt{S}}=\frac{q}{c}$,$\frac{3}{\sqrt{S}}=\frac{p}{c}$,$\frac{7}{\sqrt{S}}=\frac{r}{c}$.
三式相加得 $\frac{2+3+7}{\sqrt{S}}=\frac{p+q+r}{c}=\frac{c}{c}=1$.
所以 $\sqrt{S}=12$,$S=144$.
答案
解析
备注