三个圆,半径都是3.中心分别在 $\left( 14, 92 \right)$,$\left( 17 ,76 \right)$ 和 $\left( 19, 84 \right)$.过点 $\left( 17, 76 \right)$ 作一条直线,使得这三个圆位于这条直线某一侧的部分的面积和等于这三个圆位于这条直线另一侧的部分的面积和,求这条直线的斜率的绝对值.
【难度】
【出处】
1984年第2届美国数学邀请赛(AIME)
【标注】
【答案】
24
【解析】
首先注意到这三个圆是互相外离的等圆.如图所示,圆心 ${{O}_{1}}\left(14 ,92 \right)$,${{O}_{2}}\left( 19 ,84 \right)$,${{O}_{3}}\left( 17, 76 \right)$.由于过 ${{O}_{3}}$ 的直线总把 $\odot {{O}_{3}}$ 分为等积的两部分,因此,只需考虑过平面上怎样一点任画一条直线.对于 $\odot{{O}_{1}}$ 和 ${{O}_{2}}$ 来说,直线两侧的面积相等.显然,${{O}_{1}}{{O}_{2}}$ 的中点 $M\left(16.5 ,88 \right)$ 是二等圆 $\odot {{O}_{1}}$ 和 $\odot {{O}_{2}}$ 的中心对称中心.过 $M$ 点画的任一直线均可满足上述要求.因此,过 $M\left(16.5 ,88 \right)$ 与 ${{O}_{3}}\left( 17, 76 \right)$ 的直线即为所求,它的斜率 $k=\frac{88-76}{16.5-17}=-24$.
从图中可以看到,所求直线是唯一的,它的斜率的绝对值等于24.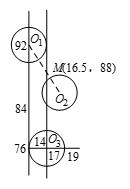
从图中可以看到,所求直线是唯一的,它的斜率的绝对值等于24.

答案
解析
备注