在四面体 $ABCD$ 中，$AB$ 棱长是 $3\operatorname{cm}$，$ABD$ 面的面积是 $15{{\operatorname{cm}}^{2}}$，$ABD$ 面的面积是 $12{{\operatorname{cm}}^{2}}$，这两个面的夹角是 $30{}^\circ $，求四面体的体积（以 ${{\operatorname{cm}}^{3}}$ 为单位）．
【难度】
【出处】
1984年第2届美国数学邀请赛（AIME）
【标注】
【答案】
$20{{\operatorname{cm}}^{3}}$
【解析】
如图所示，设 $V$ 是四面体 $ABCD$ 的体积，$h$ 是由 $D$ 引向底面 $ABC$ 上的高，则 $V=\frac{1}{3}h{{S}_{\vartriangle ABC}}$．只要确定 $h$ 即可确定 $V$．过 $D$ 作 $DK\bot AB$ 于 $K$，连 $KH$．由三垂线定理的逆定理知 $HK\bot AB$，所以 $\angle DKH=30{}^\circ $．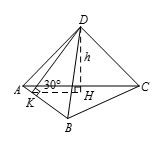
由 ${{S}_{\vartriangle ABD}}=\frac{1}{2}DK\cdot AB$，得 $DK=\frac{2{{S}_{\vartriangle ABD}}}{3}=8$．所以
$h=8\sin30{}^\circ =4$，$V=\frac{1}{3}\times 4\times 15=20\left( {{\operatorname{cm}}^{3}}\right)$
由 ${{S}_{\vartriangle ABD}}=\frac{1}{2}DK\cdot AB$，得 $DK=\frac{2{{S}_{\vartriangle ABD}}}{3}=8$．所以$h=8\sin30{}^\circ =4$，$V=\frac{1}{3}\times 4\times 15=20\left( {{\operatorname{cm}}^{3}}\right)$
答案
解析
备注
