如图所示，把单位正方形的每边分为 $n$ 等分，再连接每个顶点与其相对顶点最近的分点，这样的正方形的内部作出了一个小正方形，如果小正方形（图中用阴影表示）的面积恰好是 $\frac{1}{1985}$，求 $n$ 的值．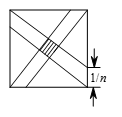
【难度】
【出处】
1985年第3届美国数学邀请赛（AIME）
【标注】
【答案】
32
【解析】
如图所示，过点 $E$ 作 $EH\bot DG$ 于 $H$，由已知 $DM=\frac{n-1}{n}$，所以 $AM=\sqrt{{{1}^{2}}+{{\left(\frac{n-1}{n} \right)}^{2}}}$，
$\cos \angle DEH=\cos \angle DAM=\frac{DA}{AM}=\frac{1}{\sqrt{1+{{\left( 1-\frac{1}{n} \right)}^{2}}}}$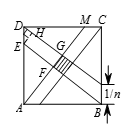
中间小正方形面积为 $S=G{{F}^{2}}=E{{H}^{2}}={{\left(DE\cdot \cos \angle DEH \right)}^{2}}=\frac{1}{1+{{\left( 1-\frac{1}{n}\right)}^{2}}}\cdot \frac{1}{{{n}^{2}}}=\frac{1}{1985}$，
即 $2{{n}^{2}}-2n+1=1984$．解得 ${{n}_{1}}=32$，${{n}_{2}}=-31$（舍）．
所以 $n=32$．
$\cos \angle DEH=\cos \angle DAM=\frac{DA}{AM}=\frac{1}{\sqrt{1+{{\left( 1-\frac{1}{n} \right)}^{2}}}}$
中间小正方形面积为 $S=G{{F}^{2}}=E{{H}^{2}}={{\left(DE\cdot \cos \angle DEH \right)}^{2}}=\frac{1}{1+{{\left( 1-\frac{1}{n}\right)}^{2}}}\cdot \frac{1}{{{n}^{2}}}=\frac{1}{1985}$，即 $2{{n}^{2}}-2n+1=1984$．解得 ${{n}_{1}}=32$，${{n}_{2}}=-31$（舍）．
所以 $n=32$．
答案
解析
备注
