在某一个圆中长度为2,3,4的平行弦分别对应于圆心角 $\alpha $,$\beta $,$\alpha +\beta $,其中 $\alpha +\beta <\text{ }\!\!\pi\!\!\text{ }$.如果把 $\cos \alpha $(这是一个正有理数)化成既约(最简)分数,问分子和分母之和是多少?
【难度】
【出处】
1985年第3届美国数学邀请赛(AIME)
【标注】
【答案】
49
【解析】
因为同圆中等弦所对的圆心角相等,所以这几条弦的平行性是无关紧要的.我们可以如图选取 $A$,$B$,$C$ 各点,使 $AB=2$,$BC=3$,因为 $\overset\frown{AC}$ 的度数等于 $\alpha +\beta $,所以必有 $AC=4$,从 $\angle ACB=\frac{\alpha }{2}$,用余弦定理可得
$\cos \frac{\alpha}{2}=\frac{A{{C}^{2}}+B{{C}^{2}}-A{{B}^{2}}}{2\cdot AC\cdot BC}=\frac{{{4}^{2}}+{{3}^{2}}-{{2}^{2}}}{2\cdot 4\cdot 3}=\frac{7}{8}$.
于是 $\cos \alpha =2{{\cos}^{2}}\frac{\alpha }{2}-1=2\cdot \frac{49}{64}-1=\frac{17}{32}$.
这正是一个既约分数,所以分子与分母之和为 $17+32=49$.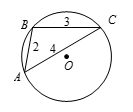
$\cos \frac{\alpha}{2}=\frac{A{{C}^{2}}+B{{C}^{2}}-A{{B}^{2}}}{2\cdot AC\cdot BC}=\frac{{{4}^{2}}+{{3}^{2}}-{{2}^{2}}}{2\cdot 4\cdot 3}=\frac{7}{8}$.
于是 $\cos \alpha =2{{\cos}^{2}}\frac{\alpha }{2}-1=2\cdot \frac{49}{64}-1=\frac{17}{32}$.
这正是一个既约分数,所以分子与分母之和为 $17+32=49$.

答案
解析
备注