三个 $12\operatorname{cm}\times 12\operatorname{cm}$ 的正方形都被连接两条邻边的中点的直线分成 $A$,$B$ 两片,如图所示.把这六片粘在一个正六边形的外面,然后折成多面体,求这个多面体的体积(单位:${{\operatorname{cm}}^{3}}$).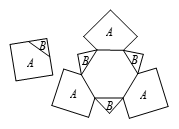

【难度】
【出处】
1985年第3届美国数学邀请赛(AIME)
【标注】
【答案】
$864{{\operatorname{cm}}^{3}}$
【解析】
折成多面体如图中(a)所示,图中标有 $P$,$Q$,$R$,$S$ 的顶点处,三个面角都是 $90{}^\circ$.由此可以认定,此多面体是正方体的一部分.可以想象得到一个边长为 $12\operatorname{cm}$ 的正方体,如图(b)作截面(过有关的六个棱的中点),恰将正方体分成两个如第一个图的多面体.立方体的体积为 ${{12}^{3}}=1728\left({{\operatorname{cm}}^{3}} \right)$,故所求多面体体积为 $\frac{1728}{2}=864\left({{\operatorname{cm}}^{3}} \right)$.

答案
解析
备注