如图所示,在 $\vartriangle ABC$ 中,$AB=425$,$BC=450$,$CA\text{=}510$,$P$ 在三角形的内部,$DE$,$FG$,$HI$ 都过 $P$ 点,长度都为 $d$,分别平行于 $AB$,$BC$,$CA$,求 $d$.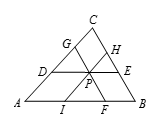

【难度】
【出处】
1986年第4届美国数学邀请赛(AIME)
【标注】
【答案】
306
【解析】
如图所示,$EH=EC-\left( BE+HC \right)=BC-\left( FP+PG \right)=450-d$.
同理 $GD=510-d$.
由 $\vartriangle DPG\backsim \vartriangle ABC$ 得 $DP=\frac{AB}{GA}\cdot GD=\frac{425}{510}\left( 510-d\right)=425-\frac{5}{6}d$.
又由 $\vartriangle PEH\backsim \vartriangle ABC$ 得 $PE=\frac{AB}{BC}\cdot EH=\frac{425}{450}\left( 450-d\right)=425-\frac{17}{18}d$,
所以 $d=DP+PE=850-\frac{16}{9}d$,$d=306$.
同理 $GD=510-d$.
由 $\vartriangle DPG\backsim \vartriangle ABC$ 得 $DP=\frac{AB}{GA}\cdot GD=\frac{425}{510}\left( 510-d\right)=425-\frac{5}{6}d$.
又由 $\vartriangle PEH\backsim \vartriangle ABC$ 得 $PE=\frac{AB}{BC}\cdot EH=\frac{425}{450}\left( 450-d\right)=425-\frac{17}{18}d$,
所以 $d=DP+PE=850-\frac{16}{9}d$,$d=306$.
答案
解析
备注