令 $\vartriangle ABC$ 为 $xy$ 一平面上的直角三角形，$C$ 为直角，弦 $AB$ 长为60，从 $A$ 和 $B$ 引出的中线分别在直线 $y=x+3$，$y=2x+4$ 上，求 $\vartriangle ABC$ 的面积．
【难度】
【出处】
1986年第4届美国数学邀请赛（AIME）
【标注】
【答案】
400
【解析】
本题中 $r=\frac{60}{2}=30$．由图（a）易算出 $\tan \theta =\frac{1}{3}$，$\sin \theta=\frac{1}{\sqrt{10}}$．如图（b）所示，取三边中点 $M$，$N$，$O$，$D$ 为重心，$p$，$q$，$s$，$t$ 的意义如图（b）所示，$\angle\theta =\angle ADM$．
$\tan\theta =\frac{1}{3}$，$\sin \theta =\frac{1}{\sqrt{10}}$．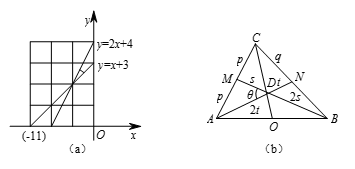
已如上所求．
由于 ${{S}_{\vartriangle ABC}}=6{{S}_{\vartriangle ADM}}$，所以 ${{S}_{\vartriangle ABC}}=6st\sin \theta =\frac{6}{\sqrt{10}}st$．（5）
又由于 $\angle C=90{}^\circ $，所以 ${{S}_{\vartriangle ABC}}=2pq$．（6）
由勾股定理得
$4{{p}^{2}}+4qh2=A{{B}^{2}}=3600$，
${{p}^{2}}+4{{q}^{2}}=9{{s}^{2}}$，
$4{{p}^{2}}+{{q}^{2}}=9{{t}^{2}}$．
利用（5），（6）得
$S_{\vartriangle ABC}^{2}=\frac{18}{5}{{s}^{2}}{{t}^{2}}=\frac{18}{5}\cdot\frac{{{p}^{2}}+4{{q}^{2}}}{9}\cdot \frac{4{{p}^{2}}+{{q}^{2}}}{9}$
$=\frac{2}{45}\left( {{\left(2{{p}^{2}}+2{{q}^{2}} \right)}^{2}}+9{{p}^{2}}{{q}^{2}} \right)$
$=\frac{2}{45}\left( {{\left( \frac{3600}{2}\right)}^{2}}+\frac{9}{4}S_{\vartriangle ABC}^{2} \right)$
$\text{=}144000\text{+}\frac{1}{10}S_{\vartriangle ABC}^{2}$，
因此 $\frac{9}{10}S_{\vartriangle ABC}^{2}=144000$，${{S}_{\vartriangle ABC}}=400$．
$\tan\theta =\frac{1}{3}$，$\sin \theta =\frac{1}{\sqrt{10}}$．
已如上所求．由于 ${{S}_{\vartriangle ABC}}=6{{S}_{\vartriangle ADM}}$，所以 ${{S}_{\vartriangle ABC}}=6st\sin \theta =\frac{6}{\sqrt{10}}st$．（5）
又由于 $\angle C=90{}^\circ $，所以 ${{S}_{\vartriangle ABC}}=2pq$．（6）
由勾股定理得
$4{{p}^{2}}+4qh2=A{{B}^{2}}=3600$，
${{p}^{2}}+4{{q}^{2}}=9{{s}^{2}}$，
$4{{p}^{2}}+{{q}^{2}}=9{{t}^{2}}$．
利用（5），（6）得
$S_{\vartriangle ABC}^{2}=\frac{18}{5}{{s}^{2}}{{t}^{2}}=\frac{18}{5}\cdot\frac{{{p}^{2}}+4{{q}^{2}}}{9}\cdot \frac{4{{p}^{2}}+{{q}^{2}}}{9}$
$=\frac{2}{45}\left( {{\left(2{{p}^{2}}+2{{q}^{2}} \right)}^{2}}+9{{p}^{2}}{{q}^{2}} \right)$
$=\frac{2}{45}\left( {{\left( \frac{3600}{2}\right)}^{2}}+\frac{9}{4}S_{\vartriangle ABC}^{2} \right)$
$\text{=}144000\text{+}\frac{1}{10}S_{\vartriangle ABC}^{2}$，
因此 $\frac{9}{10}S_{\vartriangle ABC}^{2}=144000$，${{S}_{\vartriangle ABC}}=400$．
答案
解析
备注
