如图所示,矩形 $ABCD$ 被5条线段分成4个等积的部分,且 $XY=YB+BC+CZ=ZW=WD+DA+AX$,$PQ\parallel AB$.若 $BC=19\text{cm}$,$PQ=87\operatorname{cm}$,求 $AB$ 的长度(用 $\operatorname{cm}$ 表示).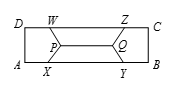

【难度】
【出处】
1987年第5届美国数学邀请赛(AIME)
【标注】
【答案】
$193\operatorname{cm}$
【解析】
因为梯形 $XYQP$ 和梯形 $ZWPQ$ 等积,且 $XY=WZ$,因回它们的高均等于 $\frac{BC}{2}$.又 $XY$ 为矩形 $ABCD$ 的周长的 $\frac{1}{4}$,因此 $XY=\frac{AB+BC}{2}$.由 $\frac{\left( PQ+XY \right)}{2}\times \frac{BC}{2}=\frac{AB\cdot BC}{4}$,得 $PQ+XY=AB$,$PQ+\frac{AB+BC}{2}=AB$,所以 $AB=BC+2PQ=193\operatorname{cm}$.
答案
解析
备注