查看数据源：5c6a5ecc210b281db9f4c7d9
如图所示，在 $5\times 5$ 的正方形中有21个空位子．已知可以在空位上填上正整数，使得各行各列都组成等差数列．问图中打星号的空格上必须填什么数字？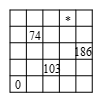
【难度】
【出处】
1988年第6届美国数学邀请赛（AIME）
【标注】
  • 知识点
    >
    数列
    >
    等差数列及其性质
    >
    等差数列的定义与通项
  • 知识点
    >
    数列
    >
    等比数列及其性质
    >
    等比数列的定义与通项
【答案】
142
【解析】
【解析】设下图中的 $a$ 和 $b$ 为所填入的两个数，由等差数列的性质可推出，第三行的公差为 $b-2a$，从上数第四行的公差为 $2b-a-74$，由此得
$\begin{matrix}\hline
{} & {} & {} & * & {} \\
\hline
{} & 74& {} & {} & {} \\
\hline
2a & b& {} & {} & 186 \\
\hline
a & 2b-74& 103 & {} & {} \\
\hline
0 & {}& {} & {} & {} \\
\hline
\end{matrix}$
$\begin{matrix}\hline
52 & 82& 112 & 142 & 172 \\
\hline
39 & 74& 109 & 144 & 179 \\
\hline
26 & 66& 106 & 146 & 186 \\
\hline
13 & 58& 103 & 148 & 193 \\
\hline
0 & 50& 100 & 150 & 200 \\
\hline
\end{matrix}$
$2a+4\left( b-2a \right)=186$
及
$a+2\left( 2b-a-74 \right)=103$．
解上述方程组，得 $a=13$，$b=66$，这样整个第三行、第四行以至第四列便都知道了．不难得到该图中各空的数字．可见，打星号处应填入142．
答案 解析 备注
0.114865s