在 $\vartriangle ABC$ 中，$\tan \angle CAB=\frac{22}{7}$，从 $A$ 引 $BC$ 的垂线把 $BC$ 分为长为3和17两段，问 $\vartriangle ABC$ 的面积是多少？
【难度】
【出处】
1988年第6届美国数学邀请赛（AIME）
【标注】
【答案】
110
【解析】
设 $x$ 为高的长，交 $BC$ 于 $D$（如图），则由 $\angle BAC=\angle BAD+\angle DAC$ 得
$\arctan\frac{22}{7}=\arctan \frac{3}{x}+\arctan \frac{17}{x}$．（5）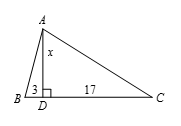
式（5）两边取正切，再应用 $\tan \left( \alpha +\beta \right)$ 的公式可得 $\frac{22}{7}=\frac{\frac{3}{x}+\frac{17}{x}}{1-\left( \frac{3}{x}\right)\left( \frac{17}{x} \right)}$．
化简得 $11{{x}^{2}}-70x-561=\left(x-11 \right)\left( 11x+51 \right)=0$．
由 $x>0$，知 $11x+51>0$，得 $x=11$．故 ${{S}_{\vartriangle ABC}}=\frac{1}{2}\left( 3+17 \right)\times 11=110$．
$\arctan\frac{22}{7}=\arctan \frac{3}{x}+\arctan \frac{17}{x}$．（5）
式（5）两边取正切，再应用 $\tan \left( \alpha +\beta \right)$ 的公式可得 $\frac{22}{7}=\frac{\frac{3}{x}+\frac{17}{x}}{1-\left( \frac{3}{x}\right)\left( \frac{17}{x} \right)}$．化简得 $11{{x}^{2}}-70x-561=\left(x-11 \right)\left( 11x+51 \right)=0$．
由 $x>0$，知 $11x+51>0$，得 $x=11$．故 ${{S}_{\vartriangle ABC}}=\frac{1}{2}\left( 3+17 \right)\times 11=110$．
答案
解析
备注
