矩形 $ABCD$ 的边长 $AB$ 为4，$CB$ 为3．用点 $A={{P}_{0}}$，${{P}_{1}}$，…，${{P}_{168}}=B$ 将 $AB$ 平分为168份；用点 $C={{Q}_{0}} {{Q}_{1}} \cdots {{Q}_{168}}=B$ 将 $CB$ 平分为168份．对 $1\leqslant k\leqslant 167$，连接线段 ${{P}_{k}}{{Q}_{k}}$．对于边 $AD$ 和 $CD$ 重复这样的工作并连接对角线 $AC$．求这335条平行线段的长度和．
【难度】
【出处】
1991年第9届美国数学邀请赛（AIME）
【标注】
【答案】
840
【解析】
如图所示，由对称性，这335条线段的长度和为 $\displaystyle AC+2\sum\limits_{K=1}^{167}{{{P}_{k}}{{Q}_{k}}}$．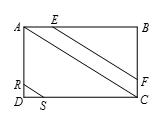
对 $1\leqslant k\leqslant 167$，有 ${{P}_{k}}B=AB\left(1-\frac{k}{168} \right)$，$B{{Q}_{k}}=BC\left( 1-\frac{k}{168} \right)$．
据此推知 $\vartriangle{{P}_{k}}B{{Q}_{k}}\backsim \vartriangle ABC$．所以有 ${{P}_{k}}{{Q}_{k}}=AC\left(1-\frac{k}{168} \right)$．
于是，这335条线段的长度和为 $\displaystyle AC\left[ 1+2\sum\limits_{k=1}^{167}{\left( 1-\frac{k}{168} \right)}\right]=5\left( 1+\frac{2}{168}\sum\limits_{i=1}^{167}{j} \right)=840$．
对 $1\leqslant k\leqslant 167$，有 ${{P}_{k}}B=AB\left(1-\frac{k}{168} \right)$，$B{{Q}_{k}}=BC\left( 1-\frac{k}{168} \right)$．据此推知 $\vartriangle{{P}_{k}}B{{Q}_{k}}\backsim \vartriangle ABC$．所以有 ${{P}_{k}}{{Q}_{k}}=AC\left(1-\frac{k}{168} \right)$．
于是，这335条线段的长度和为 $\displaystyle AC\left[ 1+2\sum\limits_{k=1}^{167}{\left( 1-\frac{k}{168} \right)}\right]=5\left( 1+\frac{2}{168}\sum\limits_{i=1}^{167}{j} \right)=840$．
答案
解析
备注
