有多少个实数 $x$ 满足方程 $\frac{1}{5}{{\log }_{2}}x=\sin \left( 5\text{ }\!\!\pi\!\!\text{ }x \right)$？
【难度】
【出处】
1991年第9届美国数学邀请赛（AIME）
【标注】
【答案】
159
【解析】
因为对任意的实数 $\theta $，都有 $\left| \sin \theta \right|\le1$，所以只需考虑那些使 $\left| \frac{1}{5}{{\log }_{2}}x \right|\leqslant 1$ 的 $x$．解得 $\frac{1}{32}\leqslant x\leqslant 32$．
首先考虑 $\frac{1}{32}\leqslant x<1$，这时 $-1\leqslant {{\log }_{2}}x<0$，而对 $\sin \left(5\text{ }\!\!\pi\!\!\text{ }x \right)$ 来说，只有当 $\frac{1}{5}\leqslant x\leqslant \frac{2}{5}$ 和 $\frac{3}{5}\leqslant x\leqslant \frac{4}{5}$ 时，才有 $\sin \left(5\text{ }\!\!\pi\!\!\text{ }x \right)\leqslant 0$，由此可知，$y=\frac{1}{5}{{\log}_{2}}x$ 和 $y=\sin \left( 5\text{ }\!\!\pi\!\!\text{ }x \right)$ 的图像在 $\frac{1}{32}\leqslant x<1$ 的范围内只能有四个交点（如图）．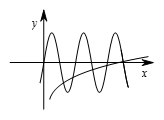
当 $1<x\leqslant 32$ 时，$0<\frac{1}{5}{{\log}_{2}}x\leqslant 1$，而对 $\sin \left( 5\text{ }\!\!\pi\!\!\text{ }x \right)$ 来说，只有当 $\frac{2k}{5}\leqslant k\leqslant \frac{2k+1}{5}$
$\left( k=3 \\ 4 \cdots 79 \right)$ 时才有 $\sin \left( 5\text{ }\!\!\pi\!\!\text{ }x \right)\geqslant 0$，在这77个区间的每一个中，两个函数图像相交于两个点．这样，在 $1<x\leqslant 32$ 内的图像一共有 $2\times 77=154$ 个交点．
当 $x=1$ 时，两函数图像也相交，所以，方程总共有 $4+154+1=159$ 个解．
首先考虑 $\frac{1}{32}\leqslant x<1$，这时 $-1\leqslant {{\log }_{2}}x<0$，而对 $\sin \left(5\text{ }\!\!\pi\!\!\text{ }x \right)$ 来说，只有当 $\frac{1}{5}\leqslant x\leqslant \frac{2}{5}$ 和 $\frac{3}{5}\leqslant x\leqslant \frac{4}{5}$ 时，才有 $\sin \left(5\text{ }\!\!\pi\!\!\text{ }x \right)\leqslant 0$，由此可知，$y=\frac{1}{5}{{\log}_{2}}x$ 和 $y=\sin \left( 5\text{ }\!\!\pi\!\!\text{ }x \right)$ 的图像在 $\frac{1}{32}\leqslant x<1$ 的范围内只能有四个交点（如图）．
当 $1<x\leqslant 32$ 时，$0<\frac{1}{5}{{\log}_{2}}x\leqslant 1$，而对 $\sin \left( 5\text{ }\!\!\pi\!\!\text{ }x \right)$ 来说，只有当 $\frac{2k}{5}\leqslant k\leqslant \frac{2k+1}{5}$$\left( k=3 \\ 4 \cdots 79 \right)$ 时才有 $\sin \left( 5\text{ }\!\!\pi\!\!\text{ }x \right)\geqslant 0$，在这77个区间的每一个中，两个函数图像相交于两个点．这样，在 $1<x\leqslant 32$ 内的图像一共有 $2\times 77=154$ 个交点．
当 $x=1$ 时，两函数图像也相交，所以，方程总共有 $4+154+1=159$ 个解．
答案
解析
备注
