查看数据源：5c6babbf210b281db9f4c8b8
大小相同的12个圆盘按下述方式放置在半径为1的圆周 $C$ 上：它们将 $C$ 盖住，两两不重叠，从而每一个圆盘必和与之相邻的两个圆盘相切．圆盘的放置如图所示，已知这12个圆盘的面积之和能写成 $\text{ }\!\!\pi\!\!\text{ }\left( a-b\sqrt{c} \right)$ 之形式，其中 $a b c$ 都是正整数而 $c$ 不能被任何素数的平方整除，求 $a+b+c$．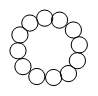
【难度】
【出处】
1991年第9届美国数学邀请赛（AIME）
【标注】
  • 知识点
    >
    数论初步
    >
    整除与同余
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的对称性
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的图象变换
  • 知识点
    >
    微积分初步
    >
    利用导数研究函数的性质
    >
    利用导数研究函数的切线
【答案】
135
【解析】
因为12个圆盘覆盖了 $C$ 而每个圆盘都与相邻的两个圆盘相切，所以 $C$ 必然通过12个切点．如图所示是一个圆盘和两个相邻圆盘的弧以及 $C$ 的一部分．设 $A$，$B$ 为切点，$P$ 为小圆盘的中心，由对称性，过 $A$，$B$ 的公切线必通过圆周 $C$ 的中心 $O$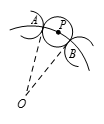，则 $\angle PBO$ 为直角，$\angle BOA=\frac{1}{12}2\text{ }\!\!\pi\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{}}{6}$，$\angle POB=\frac{\text{ }\!\!\pi\!\!\text{ }}{12}$．所以
$PB=BO\cdot\tan \angle POB=\tan \frac{\text{ }\!\!\pi\!\!\text{ }}{12}=\tan \left(\frac{\text{ }\!\!\pi\!\!\text{ }}{3}-\frac{\text{ }\!\!\pi\!\!\text{ }}{4}\right)$
$=\frac{\tan \frac{\text{ }\!\!\pi\!\!\text{}}{3}-\tan \frac{\text{ }\!\!\pi\!\!\text{ }}{4}}{1+\tan \frac{\text{}\!\!\pi\!\!\text{ }}{3}\cdot \tan \frac{\text{ }\!\!\pi\!\!\text{}}{4}}=\frac{\sqrt{3}-1}{1+\sqrt{3}}=2-\sqrt{3}$．
所以，每个圆盘的面积为 $\text{}\!\!\pi\!\!\text{ }{{\left( 2-\sqrt{3} \right)}^{2}}=\text{ }\!\!\pi\!\!\text{}\left( 7-4\sqrt{3} \right)$，
12个圆盘面积的和为 $12\text{}\!\!\pi\!\!\text{ }\left( 7-4\sqrt{3} \right)=\text{ }\!\!\pi\!\!\text{}\left( 84-48\sqrt{3} \right)$．
故 $a+b+c=84+48+3=135$．
答案 解析 备注
0.131671s