菱形 $PQRS$ 内接于矩形 $ABCD$，其中 $P$，$Q$，$R$ 和 $S$ 分别是线段 $AB$，$BC$，$CD$ 和 $DA$ 的内点（非端点），已知 $PB=15$，$BQ=20$，$PR=30$，$QS=40$．设既约分数 $\frac{m}{n}$ 为 $ABCD$ 的周长，试求 $m+n$．
【难度】
【出处】
1991年第9届美国数学邀请赛（AIME）
【标注】
【答案】
677
【解析】
如图所示，易知 $\vartriangle BPQ\vartriangle OPQ$，所以 $\angle POQ=90{}^\circ $，$P$，$O$，$Q$，$B$ 共圆，$\angle APR=\angle BQO$．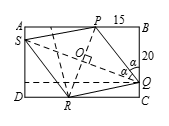
设 $\angle BQP=\angle PQO=\alpha $，则
$\sin \alpha =\frac{PB}{PQ}=\frac{3}{5}$，$\cos \alpha=\frac{4}{5}$，$\sin 2\alpha =2\times \frac{3}{5}\times \frac{4}{5}=\frac{24}{25}$，
$2\left( AB+BC \right)=2\left( SQ\sin 2\alpha +PR\sin 2\alpha \right)$
$=2\times \frac{24}{25}\times \left( 30+40\right)=\frac{672}{5}$，
所以 $m+n=677$．
设 $\angle BQP=\angle PQO=\alpha $，则$\sin \alpha =\frac{PB}{PQ}=\frac{3}{5}$，$\cos \alpha=\frac{4}{5}$，$\sin 2\alpha =2\times \frac{3}{5}\times \frac{4}{5}=\frac{24}{25}$，
$2\left( AB+BC \right)=2\left( SQ\sin 2\alpha +PR\sin 2\alpha \right)$
$=2\times \frac{24}{25}\times \left( 30+40\right)=\frac{672}{5}$，
所以 $m+n=677$．
答案
解析
备注
