如图所示，在矩形 $ABCD$ 中，$AB=12\sqrt{3}$，$BC=13\sqrt{3}$．对角线 $AC$ 和 $BD$ 相交于 $P$，若将 $\vartriangle ABP$ 剪去，然后将线段 $AP$ 和 $BP$ 叠合，并沿着线段 $CP$ 和 $DP$ 折起来，得到一个三棱锥，它的四个面都是等腰三角形，求这个三棱锥的体积．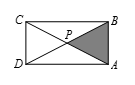
【难度】
【出处】
1990年第8届美国数学邀请赛（AIME）
【标注】
【答案】
594
【解析】
图（a），图（b）分别是矩形和三棱锥．在图（b）中，由 $PC=PD=PA$，作 $PO\bot $ 平面 $CDA$，则垂足 $O$ 为 $\vartriangle CDA$ 的外心．连 $AO$ 并处长交 $CD$ 于 $E$．因为 $CA=DA$，所以 $AE\bot CD$，$PE\bot CD$，$E$ 为 $CD$ 中点，所以
$PE=\frac{1}{2}AD=\frac{13}{2}\sqrt{3}$，$ED=\frac{1}{2}CD=6\sqrt{3}$，
$AE=\sqrt{A{{D}^{2}}-E{{D}^{2}}}=\sqrt{399}$，
${{S}_{\vartriangle CDA\left( B \right)}}=\frac{1}{2}CD\times AE=6\sqrt{3}\cdot\sqrt{399}=18\sqrt{133}$．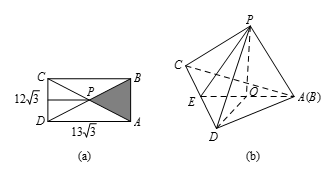
$DO$ 是 $\vartriangle CDA\left( B \right)$ 的外接圆半径 $R$，
$DO=R=\frac{abc}{4S}=\frac{13\sqrt{3}\times 13\sqrt{3}\times12\sqrt{3}}{4\times 18\sqrt{133}}=\frac{169\sqrt{3}}{2\sqrt{133}}$．
因为 $P{{O}^{2}}=P{{E}^{2}}-O{{E}^{2}}=P{{E}^{2}}+D{{E}^{2}}-D{{O}^{2}}$
$=\frac{169\times3}{4}+36\times 3-\frac{{{169}^{2}}\times 3}{4\times133}=\frac{{{99}^{2}}}{133}$，
所以 $PO=\frac{99}{\sqrt{133}}$．从而 $V=\frac{1}{3}PO\cdot{{S}_{\vartriangle ACD}}=\frac{1}{3}\times \frac{99}{\sqrt{133}}\times18\sqrt{133}=594$．
$PE=\frac{1}{2}AD=\frac{13}{2}\sqrt{3}$，$ED=\frac{1}{2}CD=6\sqrt{3}$，
$AE=\sqrt{A{{D}^{2}}-E{{D}^{2}}}=\sqrt{399}$，
${{S}_{\vartriangle CDA\left( B \right)}}=\frac{1}{2}CD\times AE=6\sqrt{3}\cdot\sqrt{399}=18\sqrt{133}$．
$DO$ 是 $\vartriangle CDA\left( B \right)$ 的外接圆半径 $R$，$DO=R=\frac{abc}{4S}=\frac{13\sqrt{3}\times 13\sqrt{3}\times12\sqrt{3}}{4\times 18\sqrt{133}}=\frac{169\sqrt{3}}{2\sqrt{133}}$．
因为 $P{{O}^{2}}=P{{E}^{2}}-O{{E}^{2}}=P{{E}^{2}}+D{{E}^{2}}-D{{O}^{2}}$
$=\frac{169\times3}{4}+36\times 3-\frac{{{169}^{2}}\times 3}{4\times133}=\frac{{{99}^{2}}}{133}$，
所以 $PO=\frac{99}{\sqrt{133}}$．从而 $V=\frac{1}{3}PO\cdot{{S}_{\vartriangle ACD}}=\frac{1}{3}\times \frac{99}{\sqrt{133}}\times18\sqrt{133}=594$．
答案
解析
备注
